Ce cours de maths, présente les Opérations sur les dérivées de fonctions : Somme de fonctions, Produit de fonctions, Quotient de deux fonctions et les fonctions composées.

Contenu

Opérations sur les dérivées de Fonctions:

La première des opérations sur les dérivées que nous allons voir, est la dérivée de la somme de fonctions.

Dérivée  Somme de Fonctions :

Supposant que la fonction f est égale à la somme de plusieurs fonctions ( h, g, i et j ) :

f  = h  +  g +  i   +  j 

Soit h, g, i et j des fonctions dérivables en x.
Donc : 

  • La fonction f est dérivable en x.
  • Le nombre dérivé au point x de la fonction f  s’écrit sous la forme suivante :

 f ‘ (x)   = h’ (x)  +  g’ (x) +  i ‘ (x) + j’ (x) 

 » Dérivée  Somme de Fonctions et la Somme des dérivées de ses fonctions « .

Exercices d’application :

Pour comprendre la dérivée d’ une somme de fonctions, nous considérons celui des fonctions Polynômes :

 1/ Exemple 1 :  Calcul dérivée de  7. x – 5 

Les dérivées des fonctions x et 2 sont respectivement 1 et 0

 (  7. x – 5 )’  =  ( 7. x ) ‘ – ( 5 ) ‘

                   = 7 ( x )’ – 0 

                   =  7 x 1 

                   = 7

( Voir Comment dériver une fonction Polynôme ?  )

 2/  Exemple 2 :   Calcul dérivée de  4.x3 + 3.x – 8

Les dérivées des fonctions x3, x et 8 sont respectivement 12.x2, 3 et 0

( 4x2 + 3x  – 8 ) ‘  = ( 4.x3 ) ‘ +  ( 3. x )’  – ( 8 ) ‘

                             = 4 ( x3 ) ‘ + 3 ( x )’  – 0

                             =  4 x 3 x x2 + 3 x 1  

                             =  12 x2  + 3

(Voir Comment dériver une fonction Polynôme ? )

Dérivée Produit de Fonctions:

La deuxième des opérations sur les dérivées de fonctions est la dérivée du Produit de fonctions.

Prenons la fonction f qui est égale au produit de deux fonctions g et h :  f  = g x h 

Soit g  et h deux fonctions dérivables en x.
Donc : 

  • La fonction f est dérivable en x.
  • Le nombre dérivé au point x de la fonction f  s’écrit sous la forme suivante :

          f ‘ (x)  =  g (x) x h‘ (x) + g’ (x) x h (x)

Exercice d’application :

Calcul dérivée de la fonction  f (x) = ( x3 + 4x – 1 ) . (x2 – 5 )

La fonction f est le produit des deux fonctions : ( x3 + 4x + 1 )  et  (x2 + 5 )

  •  Dérivée de g (x) = ( x3 + 4x – 1 )  est  3x2 + 4
  • Dérivée de h(x) = ( x2 – 5 ) est  2x

On peut donc écrire que : 

                                                                  f ‘ (x)  =  g (x) x h’ (x) + g’ (x) x h (x)

                                                                                  = ( x3 + 4x – 1 ) . ( 2x ) + ( 3x2 + 4 ) . ( x2 – 5 )

                                                                                  = 2x4 + 8x2 – 2x + 3x4 – 15x2 + 4x2 – 20

                                                                                  = 5x4 – 3x2 – 2x – 20

( Voir Comment dériver une fonction Polynôme ?  )

Dérivée Quotient de Fonctions:

La troisième des propriétés sur les dérivées de fonctions est la dérivée du quotient de fonctions.

Prenons la fonction f qui est égale au quotient de g et h :   f  = g / h 

Soit g  et h deux fonctions dérivables en x  ET  on suppose également que g est non nul en x..
Donc : 

  • La fonction f est dérivable en x.
  • Le nombre dérivé au point x de la fonction f  s’écrit sous la forme suivante :

règle calcul dérivée fonction rationnelle quotient de fonctions opérations sur les dérivées

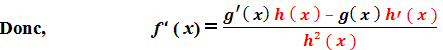
Exercice 1 : Fonction Rationnelle 

deuxieme-exemple-dune-fonction-rationnelle piger-lesmaths.fr            

Définition du domaine de définition de la fonction g :

Dg  = { x ϵ R / x – 1 ≠ 0 }

      = { x ϵ R /      x  ≠ 1 }

      = R – { 1 }

      = ] -∞ ; 1 [ U ] 1 ; + ∞[

Donc,  g est dérivable sur R – { 1 } : 

calcul-de-la-derive-dun-deuxieme-exemple-de-fonction-rationnelle

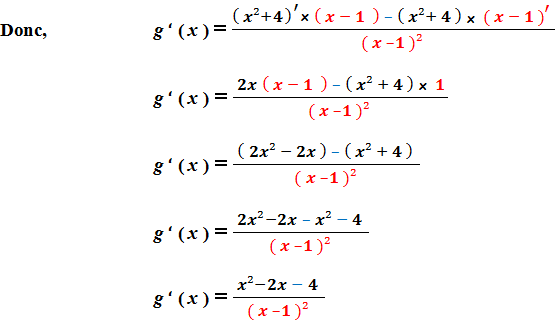
Voir Comment déterminer domaine de définition d’ une fonction rationnelle et Calcul dérivée d’ une Fonction Rationnelle )

Exercice 2 :

troisieme-exemple-dune-fonction-rationnelle

Définition du domaine de définition de la fonction h :

Dh = { x ϵ R / x² – 4x ≠ 0 }
      = { x ϵ R / x ( x – 4 ) ≠ 0 }

      = { x ϵ R /   x ≠ 0   ou   x ≠ 4  }
      = R – { 0 ; 4 }
      = ] -∞ ; 0 [ U ] 0 ; 4[ U ] 4 ; + ∞[

Donc,  h est dérivable sur R – { 0 ; 4 } : 

calculer-la-derive-du-troisieme-exemple-de-fonction-rationnelle

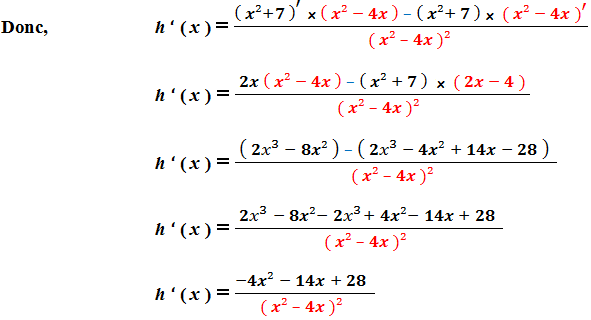
Voir Comment déterminer domaine de définition d’ une fonction rationnelle et Calcul de la dérivée d’ une Fonction Rationnelle )

Dérivée Fonctions Composées:

Théorème Dérivée Fonctions Composées:

Prenons la fonction composée g o f .

 f est une fonction dérivable en x et g est une fonction dérivable en  f (x).

La dérivée de la fonction composée  g o f au point x est :  f ‘ (x). g‘ ( f  (x) )  

Exemple d’application:

Calcul dérivée de la fonction  f (x) = sin ( 5.x3 + 1 ).

La fonction f est la fonction composée de deux fonctions dérivables sur R : 

  • g(x) = 5.x3 +1  dont la dérivée est 15.x2.
  • h(t) = sin(t)  dont la dérivée est cos(t).

f (x) = h ( g(x) )   

 f ‘ (x) =  g ‘ (x) . h’ ( g(x) )

 f ‘ (x) = ( 15.x2 ) . cos( 5.x3 +1 )

 f ‘ (x) = 15.x2. cos( 5.x3 +1 )

Si ce n’est pas encore clair pour toi sur les opérations sur les dérivées de fonctions ou comment déterminer la dérivée d’ une Somme de fonctions, Produit, Quotient, fonctions composées, n’hésite surtout pas de nous écrire en bas en commentaire. 

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

Page Facebook Pigerlesmaths

Autres liens utiles:

Opérations sur les Dérivées : Somme – Produit – Quotient – Fonctions Composées
error: Content is protected !!