Ensemble de définition d'une fonction rationnelle(quotient de 2 polynômes)

Nous allons voir dans ce cours, comment définir l’ ensemble de définition d’une fonction rationnelle à l’aide de plusieurs exemples.

Contenu

Définition d’une Fonction Rationnelle :

Une fonction rationnelle est le quotient de deux fonctions polynômes.

Exemples de Fonctions Rationnelles :

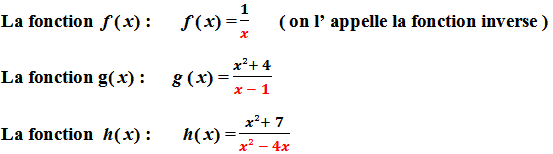
La fonction : f ( x ) : f ( x ) = ( 3x – 2 ) / ( 2x² – 5x +2 )

La fonction : g ( x ) : g( x ) = ( x² – 7x – 18 ) / ( 5x² + 3x + 14 )

La fonction : h ( x ) : h ( x ) = 2x / ( 25x² – 4 )

Ensemble de définition d’une fonction rationnelle :

Le domaine de définition d’une fonction rationnelle est Toujours R en excluant les valeurs ou s’annule le polynôme du dénominateur.

Exemple 1 : f ( x ) = 1 / x ( Fonction Inverse )

L’ensemble de définition dans ce cas est R en excluant la valeur « 0 » ou le dénominateur x s’annule.

Donc : D_f = R – { 0 } = ] -∞ ; 0 [ U ] 0 ; + ∞[ = R*

Remarque : les 3 écritures « R – { 0 } » et » ] -∞ ; 0 [ U ] 0 ; + ∞[ » et » R* » signifient la même chose.

Exemple 2 : g ( x ) = ( x² + 4 ) / ( x – 1 )

L’ensemble de définition est R en excluant les valeurs ou le dénominateur ( x – 1 ) s’annule :

Donc :

D_g = { x ϵ R / x – 1 ≠ 0 } = { x ϵ R / x ≠ 1 } = R – { 1 } = ] -∞ ; 1 [ U ] 1 ; + ∞[

Exemple 3 : h ( x ) = ( x² + 7 ) / ( x² – 4x )

x² + 7 et x² – 4x sont des polynômes.

L’ensemble de définition est R en excluant les valeurs ou le dénominateur ( x² – 4x ) s’annule.

Donc : D_h = { x ϵ R / x² – 4x ≠ 0 } = { x ϵ R / x ( x – 4 ) ≠ 0 }

On résout l’équation produit suivante : x ( x – 4 ) = 0

x ( x – 4 ) = 0
⇔ x = 0 ou x – 4 = 0
⇔ x = 0 ou x = 4

Donc : D_h = { x ϵ R / x ≠ 0 ou x ≠ 4 }
= R – { 0 ; 4 }
= ] -∞ ; 0 [ U ] 0 ; 4[ U ] 4 ; + ∞[

Exemple 4 : f ( x ) = ( 3x – 2 ) / ( 2x² – 5x +2 )

D_f = { x ∈ R / 2x² – 5x + 2 ≠ 0 }

Résolution de l’ équation du second degré : 2x² – 5x + 2 = 0 ( pour voir si des valeurs dans R ou 2x² – 5x + 2 s’ annule ).

Calcul du discriminant ∆ :

a = 2 ; b = -5 et c = 2

∆ = b² – 4ac = (-5)² – 4*2*2 = 25 – 16 = 9 > 0

Donc, l’ équation a deux solutions :

x₁ = – b – racine ( ∆ ) /2a = 5 – 3 / 2*2 = 2/-4 = 1/2

x₂ = – b + racine ( ∆ ) /-2a = 5 + 3 / 2*2 = 8/-4 = 2

Donc :

D_f = { x ∈ R / x ≠ 1/2 ou x ≠ 2 }

= R – { 1/2 ; 2 }

= ] -∞ ; 1/2 [ U ] 1/2 ; 2 [ U ] 2 ; + ∞[

Exemple 5 : h ( x ) = 2x / ( 25x² – 4 )

D_h = { x ∈ R / 25x² – 4 ≠ 0 }

= { x ∈ R / (5x)² – 2² ≠ 0 }

= { x ∈ R / ( 5x – 2 )( 5x + 2 ) ≠ 0 }

On résout l’équation produit suivante : ( 5x – 2 )( 5x + 2 ) = 0

( 5x – 2 )( 5x + 2 ) = 0
⇔ 5x – 2 = 0 ou 5x + 2= 0

⇔ 5x = 2 ou 5x = -2

⇔ x = 2/5 ou x = -2/5

Donc : D_h = { x ϵ R / x ≠ 2/5 ou x ≠ -2/5 } = R – { -2/5 ; 2/5 }

On peut aussi écrire : D_f = ] -∞ ; -2/5 [ U ] -2/5 ; 2/5 [ U ] 2/5 ; + ∞[

Exemple 6 : g ( x ) = ( x² – 7x – 18 ) / ( 5x² + 3x + 14 )

D_g = { x ∈ R / 5x² + 3x + 14 ≠ 0 }

Résolution de l’ équation du second degré : 5x² + 3x + 14 = 0 ( pour voir si y’a des valeurs dans R ou 2x² – 5x + 2 s’ annule ).

Calcul du discriminant ∆ :

a = 5 ; b = 3 et c = 14

∆ = b² – 4ac = 3² – 4*5*14 = 9 – 280 = – 271 < 0

Puisque ∆ < 0, l’ équation n’ a pas de solutions dans R.

Donc, cela veut dire que le polynôme 5x² + 3x + 14 ne s’ annule jamais dans R.

Donc : D_g = R = ] -∞ ; + ∞ [

Si ce n’est pas encore clair sur la signification de l’ ensemble de définition d’une fonction rationnelle , n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

Autres liens utiles :

Ensemble de définition d’une Fonction Rationnelle ( Quotient de Polynômes )