Contenu

Introduction : ensemble de définition d’une fonction :

Ensemble de définition d’une fonction  f  ou  Domaine de définition d’une fonction, est l’ ensemble des valeurs de x pour lesquelles la fonction  f  peut donner une image. On peut dire aussi que c’est l’ensemble des valeurs de x pour lesquelles  f ( x ) existe.

Quand on dit une fonction, ça peut être par exemple une Fonction Polynôme , Fonction Contenant la Racine Carrée,  Fonction Rationnelle., Logarithmique, Exponentielle, …etc.     

Déterminer le Domaine de définition Graphiquement  :

Ensemble de définition d’une fonction ( Trois exemples )

Exemple 1 :

La représentation graphique ci-dessous, représente une fonction  f ( x ) :

exemple de représentation graphique d'une fonction

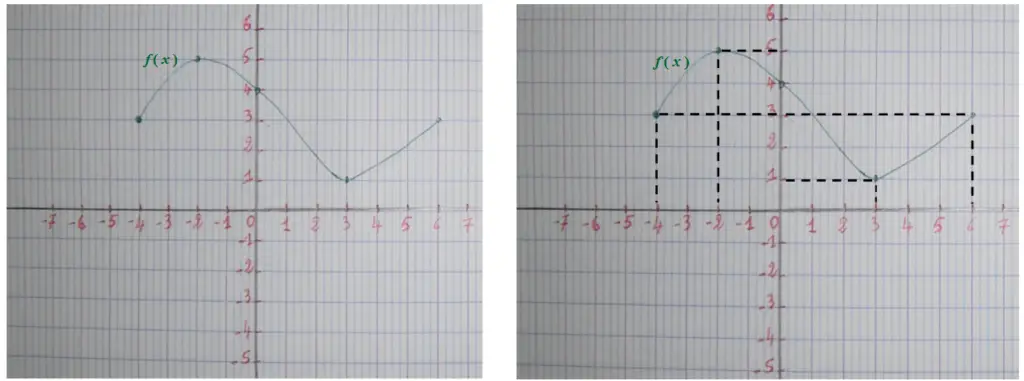
On remarque que f ( x ) existe pour toutes les valeurs de x entre -4 et 6 ( -4 et 6 inclus )

Df  signifie le domaine de définition de la fonction  f .

Donc :   Df = [ -4 ; 6 ]

Explication :

  • Pour toutes les valeurs de x < -4  f ( x ) n’existe pas.
  • Pour x = -4   on a   f ( x ) = 3
  • Pour x = -2   on a   f ( x ) = 5
  • Pour x = 0   on a    f ( x ) = 4
  • Pour x = 3   on a    f ( x ) = 1
  • Pour x = 6  on a     f ( x ) = 3
  • Pour toutes les valeurs de x > 6  f ( x ) n’existe pas.

Exemple 2 :

La représentation graphique ci-dessous, représente une fonction  g( x ) :

courbe représentative d'une fonction deuxième exemple

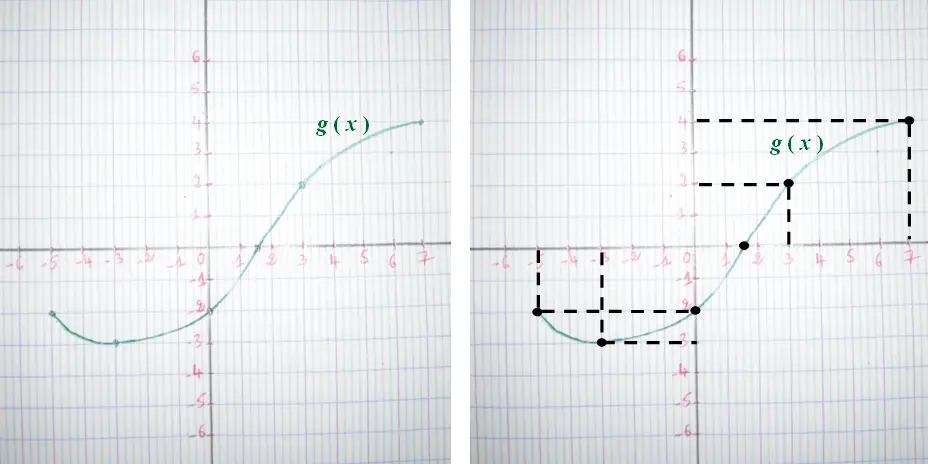
On remarque que g( x ) existe pour toutes les valeurs de x entre -5 et 7 ( -5 et 7 inclus )

Donc :   Dg = [  -5 ; 7 ]     

Dg  est le domaine de définition de la fonction g

Explication :

  • Pour toutes les valeurs de x < -5  g( x ) n’existe pas.
  • Pour  x = -5     on  a     g ( x ) = -2
  • Pour  x = -3     on  a     g ( x ) = -3
  • Pour  x = 0      on  a      g( x )  = -2
  • Pour  x = 1,5   on  a      g ( x ) = 0
  • Pour  x = 3      on  a      g ( x ) = 2
  • Pour  x = 7      on  a      g ( x ) = 4
  • Pour toutes les valeurs de x > 7  g( x ) n’existe pas.

Exemple 3 :

On considère la représentation graphique d’ une fonction  h( x ) :

ensemble de fonction troisième exemple

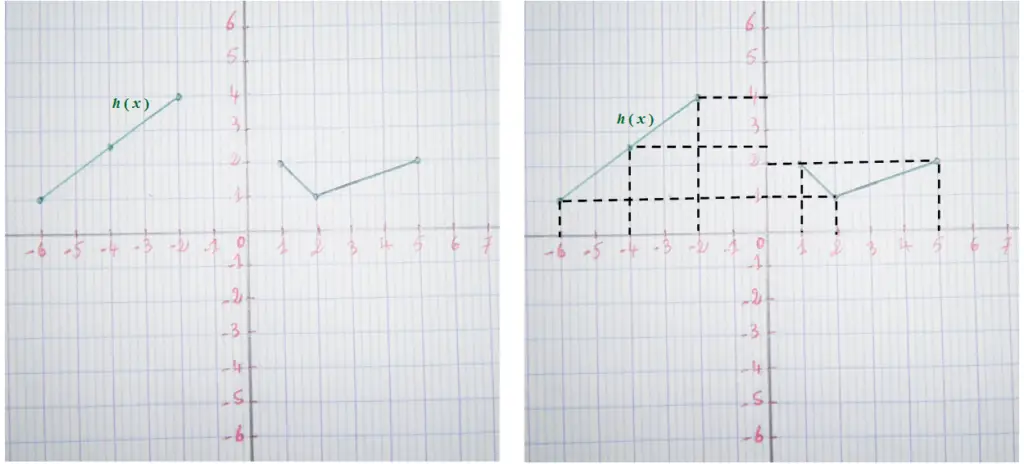
On remarque que h ( x ) existe pour toutes les valeurs de x entre -6 et -2 ( -6 et -2 inclus ) et entre 1 et 5 ( 1 et 5 inclus ).

Donc :   Dh = [ -6 ; -2 ] U [  1 ; 5 ]

 Dh  est le domaine de définition de la fonction h

Explication :

  • Pour toutes les valeurs de x < -6  h( x ) n’existe pas.
  • Pour  x = -6   on a    h ( x ) = 1
  • Pour  x = -4    on a   h ( x ) = 2,5
  • Pour  x = -2    on a   h ( x ) = 4
  • Pour toutes les valeurs de x  entre -2 et 1  h( x ) n’existe pas.
  • Pour  x = 1  on a   h( x ) = 2
  • Pour  x = 2  on a   h ( x ) = 1
  • Pour  x = 5  on a   h ( x ) = 2
  • Pour toutes les valeurs de x > 5  h( x ) n’existe pas.

Remarque IMPORTANTE :

En général, trouver l’ ensemble de définition des fonctions, est la première question qui se pose dans les exercices sur l’ étude de fonctions. Donc, savoir déterminer le domaine de définition d’une fonction est TRÈS IMPORTANT et Commettre l’ erreur à l’ensemble de définition, peut te faire perdre tous les points de l’ exercice sur l’ étude de la fonction traitée dans l’ exercice !!

Autres liens utiles :

Si ce n’est pas encore clair sur la signification de l’ ensemble de définition d’une fonction , n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

Ensemble de définition d’une fonction
error: Content is protected !!