Ensemble de définition Racine Carrée d' une fonction

Dans ce cours de maths, tu as la méthode pour déterminer l’ ensemble de définition Racine Carrée d’ une fonction est l’ ensemble des valeurs pour lesquelles la fonction est supérieur ou égal à 0.

Contenu

Ensemble de définition Racine Carrée d’ une fonction :

Quand on a une fonction f sous forme de la racine carrée, l’ ensemble de définition est l’ ensemble de valeurs pour lesquelles la fonction qu’on a à l’ intérieur de la racine, est Positif.

Exemple 1 :

L’exemple le plus simple est celui d’ une fonction racine carrée :

Les valeurs de x doivent être supérieur ou égal à 0.

On écrit : D_f= R⁺ = [ 0 ; +∞ [

Exemple 2 :

( x + 5 ) doit toujours être supérieur ou égal à 0.

Donc :

D_f = { x ϵ R / x + 5 ≥ 0 } = { x ϵ R / x ≥ -5 } = [ -5 ; + ∞ [

Exemple 3 :

( – x – 3 ) doit toujours être supérieur ou égal à 0.

Donc : D_f = { x ϵ R / – x – 3 ≥ 0 }

D_f = { x ϵ R / – x ≥ 3 }

D_f = { x ϵ R / x ≤ – 3 }

D_f = ] -∞ ; -3 ]

Fonction Racine au dénominateur d’un quotient :

Quand on a que la racine carrée au dénominateur d’une fonction, dans l’ ensemble de définition, il faut que la fonction qu’on a à l’ intérieur de la racine carrée, soit STRICTEMENT supérieure à 0 ( Strictement Positif ) pour éviter d’ avoir un dénominateur Nul. Pour mieux comprendre, tu as plusieurs exemples ci-dessous.

Nous allons déterminer le domaine de définition du quotient de deux fonctions dont le dénominateur est sous forme d’ une fonction racine carrée.

Exemple 1 :

On prend l’exemple de la fonction suivante :

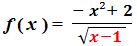
Dans ce cas, x – 1 doit être STRICTEMENT supérieur à 0 pour éviter d’avoir un dénominateur NUL.

Donc :

D_f = { x ϵ R / x – 1 > 0 } = { x ϵ R / x > 1 } = ] 1 ; + ∞ [

Donc ] 1 ; + ∞ [ est le domaine de définition de la fonction f

Exemple 2 :

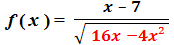
Dans ce cas, 16x – 4x² doit être STRICTEMENT supérieur à 0.

Donc : D_f = { x ϵ R / 16x – 4x² > 0 }

D_f = { x ϵ R / 4x ( 4 – x ) > 0 }

On résous l’ inéquation suivante : 4x ( 4 – x ) > 0

4x ( 4 – x ) > 0

Tableau de signes pour étudier le signe du produit 4x ( 4 – x ) :

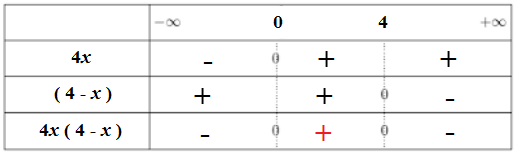
4x ( 4 – x ) > 0 à l’ intervalle ] 0 ; 4 [

Donc : D_f = ] 0 ; 4 [

Donc ] 0 ; 4 [ est le domaine de définition de la fonction f

Autres liens utiles :

Au cas où les exemples corrigés ne sont pas clairs sur comment déterminer le domaine de définition d’une fonction racine, n’hésite surtout pas de nous écrire en commentaire.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

Ensemble de définition de la racine carrée d’ une fonction