Résoudre une équation consiste à trouver les solutions qui vérifie l’équation. Nous allons voir dans cet article, comment résoudre une équation du second degré dans l’ensemble R en fonction de la valeur du discriminant ∆ ( ∆ > 0 , ∆ = 0 ou ∆ < 0 ).
Contenu
Exemples d’équations du second degré :
Une équation du second degré a la forme suivante :
a x² + b x + c = 0 avec a ≠ 0
Exemples :
3x² – 5x + 2 = 0 où a = 3 ; b = -5 et c = 2
4x² + 7 = 0 où a = 4 ; b = 0 et c = 7
7x² – 2x = 0 où a = 7 ; b = -2 et c = 0
Résoudre une équation du second degré :
Le nombre de solutions d’une équation du second degré dépend de la valeur d’un nombre appelé discriminant :
∆ = b² – 4 ac
On distingue 3 cas en fonction de la valeur du discriminant ∆ ( ∆ > 0 , ∆ = 0 et ∆ < 0 ) :
Discriminant > 0 :
L’équation a 2 solutions distinctes :
![]()
On écrit S = { x1 ; x2 }
Exemple 1:
Résoudre une équation du second degré : 3x² – 5 x + 2 = 0
Solution :
a =3 ; b = -5 et c =2
On calcule ∆ :
∆ = b² – 4 ac
= (-5)² – 4x3x2
= 25 – 24
= 1
∆ = 1 > 0 donc l’équation a 2 solutions distinctes :
![]()
![]()
Donc : S = { 1 ; 2/3 }
Exemple 2 :
Résoudre une équation du second degré : 7x² – 2x = 0
Solution :
a = 7 ; b = -2 et c = 0
On calcule ∆ :
∆ = b² – 4 ac
= (-2)² – 4x7x0
= 4 – 0
= 4
∆ = 4 > 0 donc l’équation a 2 solutions distinctes :
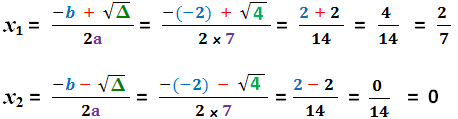
Donc : S = { 0 ; 2/7 }
Discriminant = 0 :
L’équation a une solution double :
![]()
Exemple :
Résoudre l’équation du second degré suivante : x² – 4x + 4 = 0
Solution :
a =1 ; b = -4 et c = 4
On calcule ∆ :
∆ = b² – 4 ac
= (-4)² – 4x1x4
= 16 – 16
= 0
∆ = 0 donc l’équation a une solution double :
![]()
Donc : S = { 2 }
Discriminant < 0 :
L’ équation n’a pas de solution dans R.
Exemple 1 :
Résoudre l’équation du second degré suivante : 6x² + 3x + 1 = 0
Solution :
a =6 ; b = 3 et c = 1
∆ = b² – 4 ac
= 3² – 4x6x1
= 9 – 24
= -15
∆ = -15 < 0 donc l’équation n’a pas de solutions dans R.
Exemple 2 :
Résoudre l’équation du second degré suivante : x² + x + 6 = 0
Solution :
a =1 ; b = 1 et c = 6
∆ = b² – 4 ac
= 1² – 4x1x6
= 1 – 24
= -23
∆ = -23 < 0 donc l’équation n’a pas de solutions dans R.

