Dérivée d’ une Fonction Rationnelle ( Quotient de Polynômes )

Dans ce cours, tu as la méthode du calcul de la dérivée d’ une Fonction Rationnelle ( quotient de deux polynômes ) est expliquée à l’ aide de plusieurs exemples détaillés.

Définition d’ une Fonction Rationnelle :

Une fonction rationnelle est le quotient de deux fonctions polynômes.

Calcul de la dérivée d’ une Fonction Rationnelle :

Une fonction rationnelle est dérivable sur son ensemble de définition ( Voir domaine de définition d’une Fonction Rationnelle ).

Prenons l’exemple d’une fonction rationnelle  f  : 

Pour calculer la dérivée d’une fonction rationnelle, on applique la règle suivante :

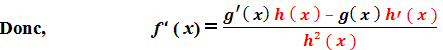
Exemple 1 :

D_f  = R – { 0 } = R*

Donc,  f  est dérivable sur R* :

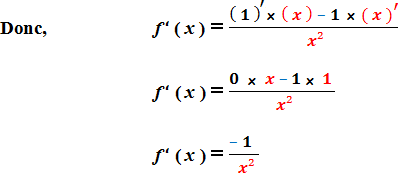
Exemple 2 :

D_g  = { x ϵ R / x – 1 ≠ 0 }

      = { x ϵ R /      x  ≠ 1 }

      = R – { 1 }

      = ] -∞ ; 1 [ U ] 1 ; + ∞[

Donc,  g est dérivable sur R – { 1 } : 

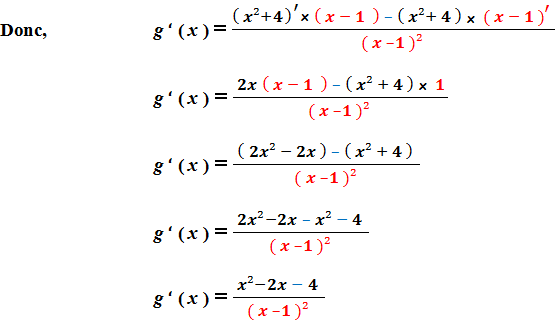
Exemple 3 :

D_h = { x ϵ R / x² – 4x ≠ 0 }
      = { x ϵ R / x ( x – 4 ) ≠ 0 }

      = { x ϵ R /   x ≠ 0   ou   x ≠ 4  }
      = R – { 0 ; 4 }
      = ] -∞ ; 0 [ U ] 0 ; 4[ U ] 4 ; + ∞[

Donc,  h est dérivable sur R – { 0 ; 4 } : 

 

 

 

 

 

 

 

 

 

---

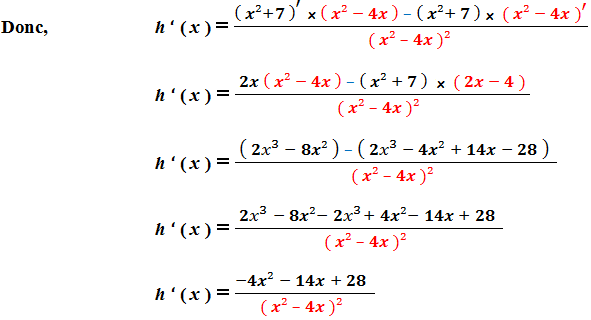
Autres liens utiles :

• Définir le domaine de définition d’ un quotient de polynômes
• Rappel sur la dérivée d’une fonction Polynôme
• Tableau de dérivées usuelles – Formules de dérivation
• Dérivée de Racine Carrée d’ une Fonction
• Calculateur de Dérivée en Ligne – Calcul Fonction Dérivée
• Page Facebook Pigerlesmaths

---

Si ce n’est pas encore clair sur comment calculer la Dérivée d’ une Fonction Rationnelle , n’hésite pas de nous écrire en commentaire et nous te répondrons le plutôt possible.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête.