Dérivée d’ un Polynôme | Cours sur les Fonctions

Dérivée d’ un polynôme (4 notions à savoir)

Calculer la dérivée d’ un polynôme, nécessite la maîtrise de 4 notions importantes qui sont faciles à comprendre :

• La dérivée de la somme de plusieurs fonctions est égal à la somme des dérivées de ces dernières : 

Prenons             f (x) = h (x) +  g (x)     

Donc :        (  f (x) )’  = ( h (x)  +  g (x) )’ = ( h (x) )’ + ( g (x) )’

• En sachant que C est une Constante : 

( C. f (x) )’ = C. (  f (x) )’

• Dérivée de ce type de fonction  f ( x ) = x ⁿ :                                               

(  f ( x ) )’ = ( x ⁿ  )’ = n. x ^n-1

• Dérivée d’une Constante C est TOUJOURS Nulle ( peu importe la valeur de la constante ) :        

( C )’ = 0

Vidéo : Calcul de la dérivée d’ un polynôme

Les deux exemples de polynômes expliqués dans la vidéo : 

3 x²  + 2 x + 1     et       7 x³  –  5 x² +  x

A la fin de la vidéo, tu as un exercice d’application.

Correction de l’ exercice (Voir la fin de la vidéo)

 1/   Premier polynôme :   9x – 2 

 ( 9x – 2 ) ‘  = 9 ( x )’ – ( 2 )’

                  = 9 x 1 + 0 

                  = 9

 2/   Deuxième polynôme :  7x ² + 3x – 8

 ( 7x² + 3x  – 8 ) ‘  =  7 ( x² ) ‘ + 3 ( x )’  – ( 8 ) ‘

                             =  7 x 2 x x + 3 x 1  –  0

                             =  14 x  + 3 

---

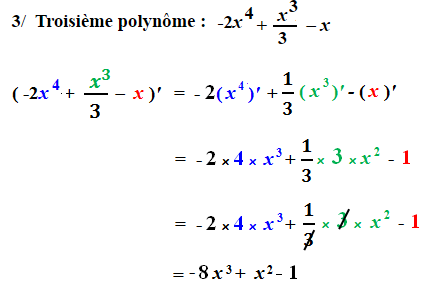
Autres liens utiles :

• Domaine de définition d’un Polynôme
• Tableau de dérivées usuelles – Formules de dérivation
• Calcul de la Dérivée d’une Fonction Rationnelle
• Dérivée de Racine Carrée d’ une Fonction
• Calculateur de Dérivée en Ligne – Calcul Fonction Dérivée

---

Si ce n’est pas encore clair sur comment calculer la dérivée d’ un polynôme , n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible.

Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête