Nous allons voir dans ce cours la méthode à suivre pour déterminer l’ équation de la tangente à une courbe à un point donné.
Contenu
Théorème : équation de la tangente à une courbe
Soit Cf la courbe représentative d’une fonction f dérivable dans un intervalle I.
Prenons le point a ∈ I. La tangente à la courbe Cf au point A( a ; f(a) ) est la droite qui passe par A et dont le coefficient directeur est f ′(a).
L’ équation de la tangente à Cf au point A d’ abscisse a est sous la forme suivante :
y = f ′(a) (x – a) + f(a)
Exercices sur l’ équation de la tangente à une courbe
Exercice 1 : Équation de la tangente à une courbe
On considère une fonction ƒ dont on ne précise pas la formule algébrique et qui est dérivable au point d’ abscisse 2 et on a f ( 2 ) = -3 et f ‘ ( 2 ) = -7
Solution :
L’ équation de la tangente à la courbe représentative de f au point d’ abscisse 2 est :
y = f ′( a ) ( x – a ) + f ( a )
⟺ y = -7 ( x – 2 ) + f ( 2 )
⟺ y = -7 x + 14 – 3
⟺ y = -7 x + 11
Exercice 2 : Équation de la tangente à une courbe
On considère la fonction f définie sur R par f ( x ) = x3 – 3x + 1
La courbe Cf représentative de f est la suivante :
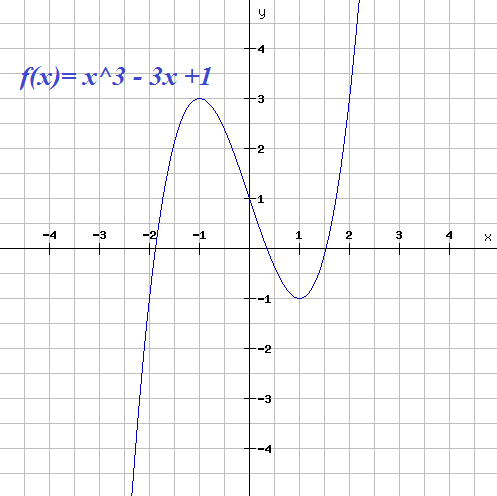
Question 1 : Déterminer les équations des tangentes aux points A et B d’abscisses respectives -2 et 0 de la courbe représentative de f .
Questions 2 : Construire les tangentes aux points A et B.
Solution :
Question 1 :
f( x ) est un polynôme. Donc, il est dérivable sur R et cela veut dire que f peut avoir une tangente au point d’ abscisse -2 et 0.
f ‘( x ) = ( x3 – 3x + 1 )’ = 3x2 – 3
Au point d’ abscisse -2 :
L’ ordonnée du point d’abscisse -2 est : f (–2) = ( -2 )3 – 3 x ( -2 ) + 1 = -8 + 6 + 1 = -1
La dérivée de f au point -2 : f ‘(–2) = 3 ( -2 )2 – 3 = 3 x 4 – 3 = 12 – 3 = 9
L’ équation de la tangente est :
y = f ′( -2 ) ( x – ( -2 ) ) + f ( -2 )
⟺ y = 9 ( x + 2 ) – 1
⟺ y = 9 x + 18 – 1
⟺ y = 9 x + 17
Donc, l’ équation de la tangente est : y = 9 x + 17
Au point d’ abscisse 0 :
L’ ordonnée du point d’abscisse 0 est : f ( 0) = 0 – 3 x 0 + 1 = 1
La dérivée de f au point 0 : f ‘( 0 ) = 3 x 0 – 3 = – 3
l’ équation de la tangente est : y = f ′( 0 ) ( x – 0 ) + f ( 0 ) = -3 x + 1
Donc, l’ équation de la tangente à la forme suivante : y = -3 x + 1
Questions 2 : Construire les tangentes aux points A et B :
( Voir Comment Représenter Graphiquement une fonction affine )
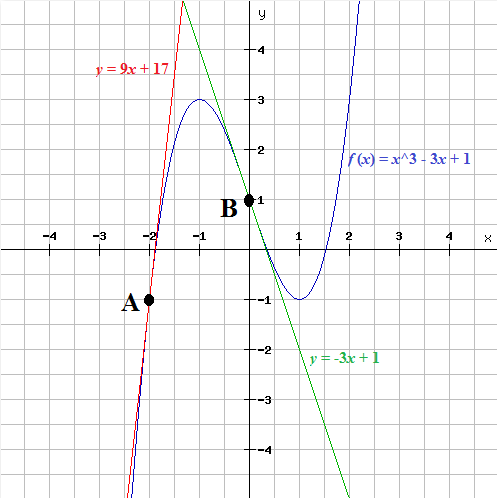
Si ce n’est pas encore clair sur l’ équation de la tangente à une courbe, n’hésite surtout pas de laisser un commentaire en bas.
Consultez aussi notre Page Facebook de Piger-lesmaths

