Contenu
Fonction Affine :
Soit a et b deux nombres non nuls.
En associant à chaque nombre » x » un nombre « a x + b » appelé image de x, on définit une Fonction Affine f.
On notera cette fonction f : x → a x + b
L’image de x sera notée f ( x ).
Fonction Affine : Déterminer l’ Image et l’Antécédent ?
Soit f la Fonction Affine définie par : f : x → 2 x + 7
Exemple 1 : L‘image de 5 par f ?
– L’image de 5 est 17 Car f ( 5 ) = 2 × 5 + 7 = 10 + 7 = 17
Et on dit que 5 est l’antécédent de 17
Exemple 2 : L’image de -3 par f ?
– L’image de (-3) est 1 Car f (– 3) = 2 × (– 3) + 7 = – 6 + 7 = 1
Et on dit que -3 est l’antécédent de 1
Exemple 3 : L‘Antécédent de 8 par f ?
– L’antécédent de 8 par f est le nombre x tel que :
2 x + 7 = 8
⟺ 2 x = 8 – 7
⟺ 2 x = 1
⟺ x = 1/2
⟺ x = 0,5
Exemple 4 : L‘Antécédent de 0 par f ?
– L’antécédent de 0 par f est le nombre x tel que :
2 x + 7 = 0
⟺ 2 x = – 7
⟺ 2 x = -7/2
⟺ x = -3.5
Donc, l’antécédent de 0 par f est 3,5 et on peut regrouper ces résultats dans un tableau :
| x | -3 | 0.5 | -3.5 | 5 |
| f (x) | 1 | 8 | 0 | 17 |
Fonction Affine : Représentation Graphique
Remarques IMPORTANTES :
- Pour représenter une droite, on a besoin d’avoir les coordonnées de 2 points.
- la Représentation Graphique d’ une Fonction Affine est sous forme d’ une Droite.
Exemple 1 :
Nous allons voir dans la vidéo ci-dessous, la représentation graphique de f ( x ) = 2 x + 1
Exemple 2 :
Nous allons voir dans la vidéo ci-dessous, la représentation graphique de f ( x ) = 3 x – 1
Exemple 3 :
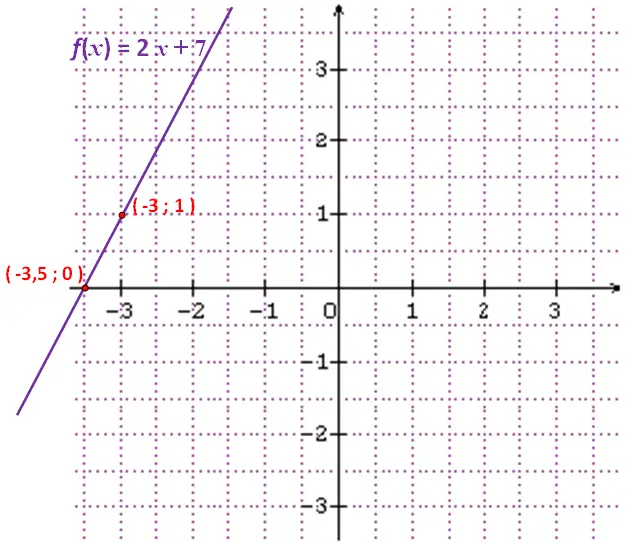
Nous allons voir la représentation graphique de f ( x ) = 2 x + 7
| x | -3 | 0.5 | -3.5 | 5 |
| f (x) | 1 | 8 | 0 | 17 |
Suivant le tableau : f ( -3 ) = 1 et f ( -3,5 ) = 0
Donc, on peut tracer la droite qui représente f ( x ) à l’aide des deux points qui ont pour coordonnées : ( -3 ; 1 ) et ( -3.5 ; 0 )
Fonction Linéaire :
Une fonction Linéaire est un Cas particulier d’une fonction Affine ( b = 0 )
On associé à chaque nombre » x » un nombre » a x » et on notera cette fonction f : x → a x
Fonction Linéaire : Déterminer l’ Image et l’Antécédent
Soit f la fonction Linéaire définie par : f : x → 5 x
Exemple 1 : L‘image de 3 par f ?
– L’image de 3 est 15 Car f ( 3 ) = 5 × 3 = 15
Et on dit que 3 est l’antécédent de 15
Exemple 2 : L‘image de -2 par f ?
– L’image de ( -2 ) est -10 Car f (– 2) = 5 × (– 2) = -10
Et on dit que -2 est l’antécédent de -10
Exemple 3 : L‘Antécédent de 9 par f ?
– L’antécédent de 9 par f est le nombre x tel que :
5 x = 9
⟺ x = 9/5
⟺ x = 1,8
Donc, l’antécédent de 9 par f est 1,8
Fonction Linéaire : Représentation Graphique
La Représentation Graphique d’ une Fonction Affine ne passe JAMAIS par l’origine du repère qui est le point O (0 ; 0). Par contre, celle d’une Fonction Linéaire passe TOUJOURS par l’origine O (0 ; 0) : Parce que, f ( 0 ) = a x 0 = 0
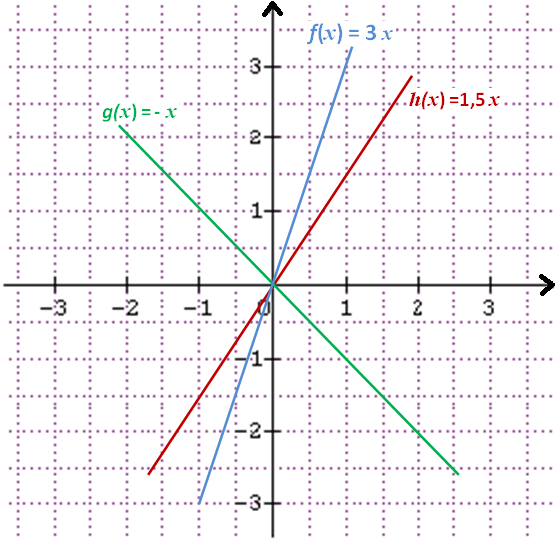
Les trois fonctions représentées graphiquement ci-dessous, sont toutes des Fonctions Linéaires :
- f (x) = 3 x
- g (x) = – x
- h (x) = 1,5 x
La vidéo ci-dessous, explique comment nous avons représenter graphiquement la fonction : f (x) = 3 x
La vidéo ci-dessous, explique comment nous avons représenter graphiquement la fonction : g (x) = – x
Explication de la Représentation Graphique des 3 fonctions :
Pour représenter f (x) = 3 x j’ai déjà le premier point O ( 0 ; 0 )
Concernant le 2ème point, je peux calculer par exemple l’image de 1 : f (1) = 3 x 1 = 3.
Donc, le 2ème point a pour coordonnées ( 1 ; 3 )
A partir de ces deux points ayant comme coordonnées ( 0 ; 0 ) et ( 1 ; 3 ), je trace la droite qui est en couleur Bleu.
Tu fais pareil pour les deux autres fonction ( g (x) et h (x) )
Autres liens utiles :
Si ce n’est pas encore clair sur la Fonction Affine et Linéaire, n’hésite surtout pas de nous laisser un commentaire en bas en commentaire.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

