FONCTION EXPONENTIELLE – Cours Maths Terminale

Fonction Exponentielle de base e

Nous allons voir dans ce cours, la fonction exponentielle : 

• Propriétés importantes à savoir surtout quand on simplifie des expressions contenant l’exponentielle;
• Dérivabilité;
• Tableau de variations, Limites en l’infini et la courbe représentative.

Définition :

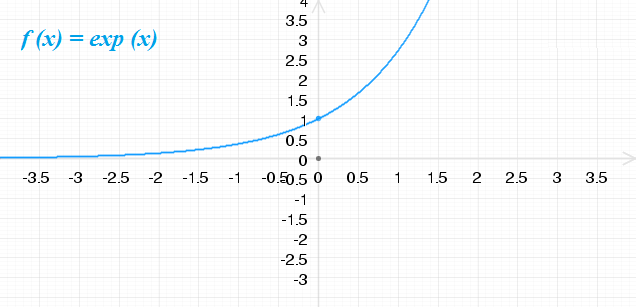
La fonction exponentielle de base e, est notée exp, telle que pour tout réel x, on a exp : x  ⟼ e^x . 

Le réel e est égal à environ 2,718  ( e = e¹ = 2.718281828 et cette valeur approchée peut être retrouvée à l’aide d’ une calculatrice scientifique ainsi que la courbe représentative ).

 

Propriétés :

a)  e⁰ = 1  et e¹= e

Dans les propriétés qui suivent, nous allons voir les mêmes propriétés déjà vu en puissances ( Voir Produit de puissances  et  Quotient de puissances ).

Pour tout x et y, on a :

b) e^x > 0

c) e^{x + y} = e^x e^y

d) e^–x = 1/e^x  et  e^x = 1/e^–x

e) e^x-y = e^x/e^y

f) (  e^x )^y = e^xy

Exercice : Simplifier des écritures contenant l’ exponentielle :

A = e⁴ × e⁻⁶ / e⁻⁷

B = ( e^-6 )⁵ × e⁻⁴

C = 1/( e^-3 )² + ( e⁴ )⁻¹ / e²  ×  e^-6

Correction :

A = e⁴ × e⁻⁶ / e⁻⁷

    = e^-2 / e⁻⁷                     ( Voir  Quotient de puissances ).

    = e⁵

B = ( e^-6 )⁵ × e⁻⁴

   =  e^-30 × e⁻⁴            ( Voir Produit de puissances ).

   =  e^-34

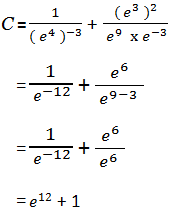     ( Voir  Quotient de puissances ).

Dérivée de la fonction exponentielle

Propriété :

La fonction exponentielle est continue et dérivable sur ℝ et (exp x)’ = ( e ^x )’ = e ^x

Exercice d’ Application :

Dériver une fonction contenant la fonction exponentielle

a) f (x) = 4x − 3e^x                          ( Voir  Dérivée de la Somme de fonctions ).

f ‘(x) = ( 4x − 3e^x )’

         = ( 4x )‘ − ( 3e^x )’ 

         = 4 – 3e^x

b) g(x) = ( x − 1)e^x

g ‘(x) = ( x − 1 )e^x                        ( Voir  Dérivée du Produit de fonctions ).

         = ( x − 1 )’ e^x + ( x − 1 ) ( e^x )’

         = 1 x e^x + ( x − 1 ) e^x 

         = e^x + ( x − 1 ) e^x 

         = ( 1 + x − 1 ) e^x  

        = x e^x

c) h(x) = e^x / x                             ( Voir  Dérivée du Quotient de fonctions ).

h'(x) = ( e^x / x )‘

         = ( ( e^x )’ x  x –  e^x x  x’  ) /  x²

         = ( e^x x  x – e^x x 1) /  x²

         = ( x e^x  – e^x ) /  x²

         = ( x  – 1 ) e^x /  x²

Variations :

Propriété :

La fonction exponentielle est strictement croissante sur ℝ.

Démonstration :

Comme (exp x )’ = exp x > 0 , la fonction exponentielle est strictement croissante.

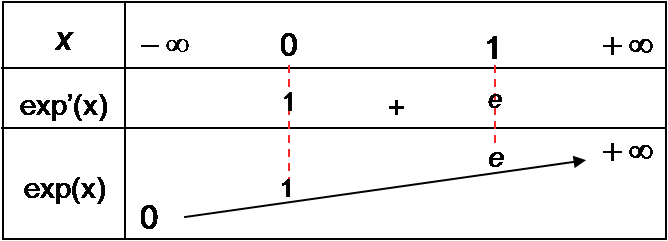
Limites en l’infini :

On dresse le tableau de variations de la fonction exponentielle :

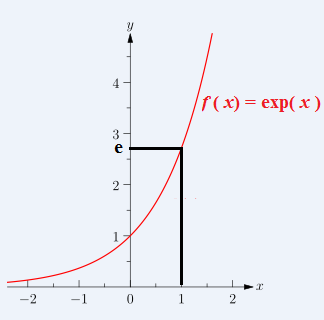
Courbe représentative : Fonction exponentielle

Exercice : Etudier une fonction exponentielle

Soit  f  la fonction définie sur ℝ par f (x) = ( x + 2 ) e^x .

a) Calculer la dérivée de la fonction f.

b) Dresser le tableau de variations de la fonction f.

c) Déterminer une équation de la tangente à la courbe au point d’abscisse 0.   ( Voir Comment déterminer l’ équation de la tangente )

d) Tracer la tangente à la courbe f 

e) Tracer la courbe représentative de la fonction f 

Correction :

a)  f ‘(x) = ( ( x + 2 ) e^x  )’                                  

             = ( x + 2 )’ e^x + ( x + 2 )( e^x )     ( Voir Dérivée du Produit de fonctions  et  Calcul de la dérivée d’ un Polynome )

             = e^x + ( x + 2 )e^x   

             = ( x + 3)e^x

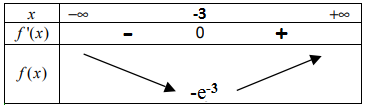
b) Comme e ^x  > 0 , le signe de f ‘(x) dépend de x + 3.

x + 3 est Négatif pour toutes les valeurs de l’intervalle ] −∞;−3 [ et Positif sur l’intervalles ] −3;+∞ [ et s’annule à x = –3.

f est donc décroissante sur l’intervalle ] −∞;−3 ] et croissante sur l’intervalle [ −3;+∞ [

Tableau de variations :

c)

f (x) = ( x + 2)e^x   et    f ‘(x) = ( x + 3)e^x

 f (0) = ( 0 + 2 )e⁰  = 2   et    f ‘(0) = ( 0 + 3)e⁰ = 3

L’ équation de la tangente à la courbe de f en 0 est donc :        ( Voir Comment déterminer l’ équation de la tangente )

y = f ‘(0) (x − 0) + f (0), soit :  y = 3x + 2

d) et e)

Soit g la fonction tangente : g(x) = 3x + 2 

Concernant la représentation graphique de la tangente et la fonction f , voir la figure suivante :

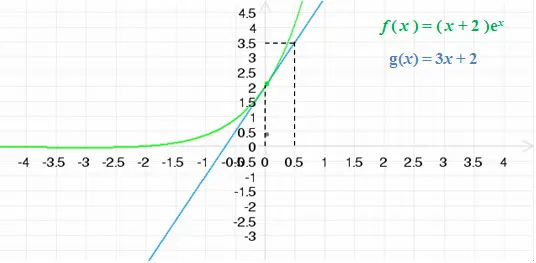
( Voir Comment Représenter graphiquement une fonction affine )

Résolution d’équations et d’inéquations

Propriétés :

Pour tout réel a et b, on a :
e^a = e^b ⇔ a = b
e^a < e^b ⇔ a < b

Exercice d’ application : Résoudre une équation ou une inéquation

a) Résoudre dans ℝ l’inéquation e^5x−1 ≥ 1.

b) Résoudre dans ℝ l’inéquation e^7x+2 > 1.

c) Résoudre dans ℝ l’équation exp(x² − 5 ) − exp(−4x ) = 0 .

Correction :

a)

         e^5x-1 ≥ 1

⇔     e^5x-1 ≥ e⁰

⇔   5x − 1 ≥ 0

⇔        5x  ≥ 1

⇔           x ≥ 1/5

L’ensemble des solutions est l’intervalle [ 1/5 ;+∞ [

b)

         e^-7x+2 > 1

⇔     e^-7x+2 > e⁰

⇔   -7x + 2  > 0

⇔        -7x   > -2

⇔            x  < -2/-7

⇔            x  < 2/7

L’ensemble des solutions est l’intervalle [ – ∞ ; 2/7 [

c)     exp(x² − 5 ) − exp( − 4x ) = 0
⇔                      exp( x² − 5 ) = exp( − 4x )            
⇔                              x² − 5   = − 4x
⇔                        x² − 5 + 4x = 0                  ( Voir Comment résoudre une équation second degré )
⇔                             x₁ = 1 ou x₂ = -5    (  ∆ = 16 – 4 * (-5) = 16 + 20 = 36   Donc  x₁ = 1 et  x₂ = -5  ) 
Les solutions sont 1 et -5.                     

Fonctions de la forme e^f(x)

Propriétés :

Propriété 1:

Soit f(x) une fonction dérivable sur un intervalle I. La fonction x ⟼ e^f(x) est dérivable sur I.

La dérivée de la fonction x ⟼ e^f(x) est la fonction x ⟼  f ‘(x)e^f(x)

Exemples :

Soit f (x) = e^6x+2 alors f ‘(x) = ( e^6x+2 ) ‘ = ( 6x+2 )’ e^6x+2 = 6e^6x+2 

Soit g (x) = e^-7x  alors g ‘(x) = ( e^-7x ) ‘ = ( -7x )’ e^-7x = -7e^-7x 

Propriété 2:

Soit f une fonction dérivable sur un intervalle I.
Les fonctions x ⟼ f(x) et x ⟼ e^{f ( x)} ont le même sens de variation.

Démonstration :

On a ( e^f(x) )’ = f ‘(x) e^f(x) Comme e^f(x)  > 0 , f ‘(x) et ( e^f(x) )’ sont de même signe.

Exemples :

La fonction x² est croissante sur ] −∞;0 ] et sur  [ 0 ; +∞ [
Donc la fonction exp(x²) est également croissante sur ] −∞;0 ] et sur  [ 0 ; +∞ [

La fonction 1/x est décroissante sur ] −∞;0 [ et sur  ] 0 ; +∞ [
Donc la fonction exp(1/x) est également décroissante sur ] −∞;0 [ et sur  ] 0 ; +∞ [

---