Agrandissement ou réduction de rapport k ( k < 1 ou k > 1 )

Définition : Agrandissement ou Réduction

Dans le cas d’ un agrandissement ou réduction de rapport k d’une figure ou d’un solide (longueurs des côtés, des arêtes, rayons), on multiplie toutes les dimensions par le nombre k strictement positif ( k > 0 ). On dit qu’on a effectué :

• Un agrandissement si k > 1
• Une réduction si k < 1

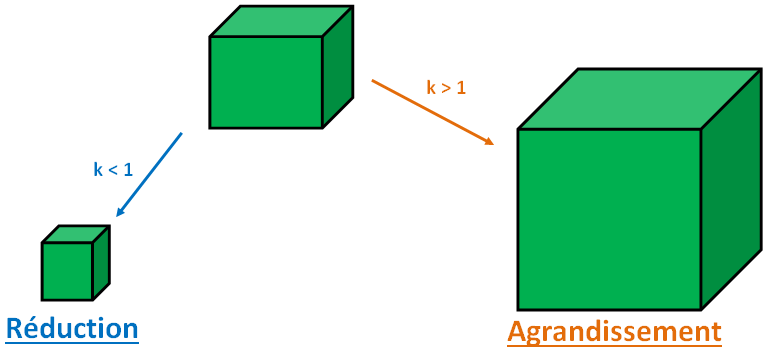
Remarque : Soit dans le cas d’ un agrandissement ou réduction, les mesures des angles de la figure sont inchangés.

Propriété 1 : Agrandir ou Réduire une figure

Quand on agrandi ou réduit un objet, on obtient un objet de même nature géométrique :  Réduire ou agrandir un carré, on obtient un carré ( c’est pareil pour un cylindre de révolution , …etc ).

Propriété 2 : Agrandissement ou réduction de rapport k

Dans un agrandissement ou réduction de rapport k :

• l’ aire d’une surface est multiplié par k² ;
• le volume d’un solide est multiplié par k³.

Exercices sur l’ agrandissement ou réduction :

Exercices 1 : ( Agrandissement d’un cube de rapport k = 3 )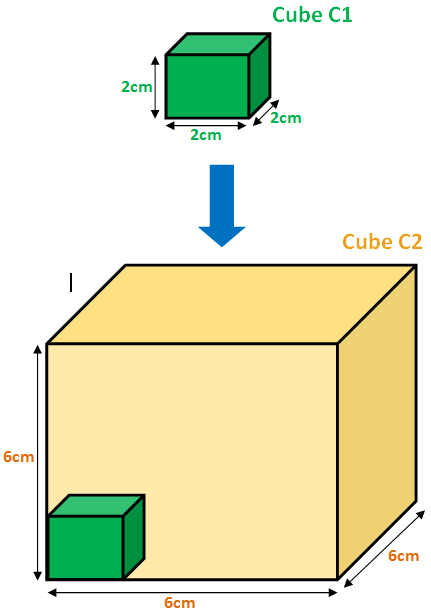

1) Calculer l’aire d’une face et le volume du cube C1.
2) On multiplie la longueur de toute les arêtes par 3 on obtient le cube C2.
   a) Quelle est la longueur des arêtes du cube C2 ?
b) Calculer l’aire de chaque face du cube C2 puis le volume de ce cube.

Solution :

L1, A1 et V1  représentent respectivement la longueur de l’arête, l’aire et le volume du cube C1.

L2, A2 et V2  représentent respectivement la longueur de l’arête, l’aire et le volume du cube C2.

1) 

Aire d’une face du cube C1 : A1 = 2² = 4 cm²
Volume du cube C1 : V1 = 2³ = 8 cm³ .

2) 
   a) 

C2 représente un agrandissement de rapport k = 3 du cube C1.

Donc :  L2 = L1 x 3 = 2 x 3 = 6 

   b)

C2 représente un agrandissement de rapport k = 3 du cube C1.

Donc : A2 = A1 x 3² = 4 x 9 =  36 cm²

            V2 = V1 x 3³ = 8 x  27 = 216 cm³

Exercice 2 : ( Réduction d’un pavé de rapport 0,6 )

Le petit pavé est une réduction du grand pavé de coefficient 0,6.

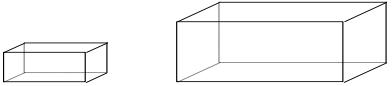
en sachant l’aire totale du grand pavé est de 648 cm², c’est quoi l’aire total du petit pavé ?

Solution :

L’aire total du grand pavé est de 648 cm². 

Donc, l’aire total du petit pavé est :

 0,6² x 648 = 0,36 x 648 = 233,28 cm²

---

Autres liens utiles sur la Géométrie :

• Formules d’Aires et de Volumes
• Polygones Réguliers

• Théorème de Pythagore ( Introduction )
• Calcul de la longueur d’un côté dans un triangle rectangle
• Réciproque du théorème de Pythagore ( Exercice d’ Application )
• Contraposée du théorème de Pythagore ( Exercice d’ Application )

• Théorème de Thalès
• Réciproque et Contraposée du théorème de Thalès

---

Si ce n’est pas encore clair ce cours sur l’ agrandissement ou réduction, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.

Consulter aussi notre Page Facebook Piger-lesmaths.