Le théorème des milieux est utilisé dans des raisonnements en géométrie et nous allons voir dans ce cours, les 3 cas de figure. Ce théorème, représente un cas particulier du Théorème de Thalès et sa Réciproque.
Contenu
Premier Théorème des milieux :
Énoncé :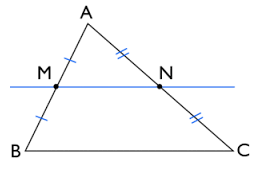
» La droite qui joint les milieux de deux côtés d’un triangle est parallèle au troisième côté « .
Dans notre cas, M et N représentent respectivement les milieux des deux côtés [AB] et [AC]
Donc, les deux droites (MN) et (BC) sont parallèles.
A quoi sert ce 1er Théorème ?
Ce théorème sert à prouver que deux droites sont parallèles.
Exo d’application ( 1er Théorème des milieux ) :
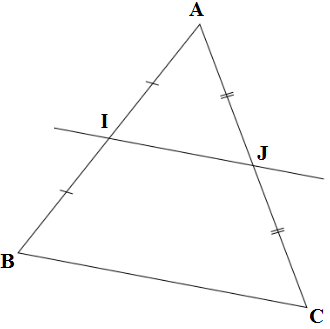
ABC est un triangle.
I et J sont respectivement les milieux des deux côtés [AB] et [AC]
Est ce que les deux droites (MN) et (BC) sont parallèles ?
Solution :
Dans le triangle ABC on a I et J sont respectivement les milieux des deux côtés [AB] et [AC]
D’après le théorème des milieux, la droite (IJ) qui passe par les deux milieux I et J est parallèle au troisième côté du triangle ABC.
Donc, (IJ) et (BC) sont parallèles.
Deuxième Théorème des milieux :
Énoncé :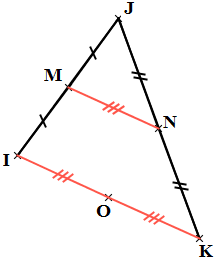
» Le segment qui joint les milieux de deux côtés d’un triangle mesure la moitié du troisième côté » .
Dans notre cas, M et N représentent respectivement les milieux des deux côtés [JI] et [JK]
Donc : MN = IK/2
Prenons O est le milieu du côté [IK]
Donc : MN = IK/2 = IO = OK
A quoi sert ce 2ème Théorème ?
Ce théorème nous permet de calculer des longueurs.
Troisième théorème des milieux :
Énoncé :
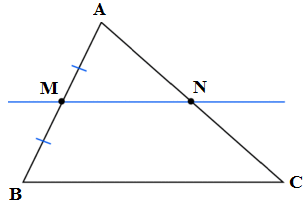
» La droite qui passe par le milieu d’un côté d’un triangle et qui est parallèle au troisième côté coupe le deuxième côté en son milieu » .
Dans notre cas :
- M représente le milieu de [AB]
- La droite ( en bleu ) passant par M et parallèle à la droite (BC), coupe le côté [AC] en N.
Donc, N représente le milieu du côté [AC].
A quoi sert ce 3ème Théorème ?
Ce théorème nous permet de prouver qu’un point est le milieu d’un segment.
Autres liens utiles :
- Calculer la longueur d’un côté dans un Triangle Rectangle
- Réciproque du Théorème de Pythagore
- Contraposée du Théorème de Pythagore
Si ce n’est pas encore clair pour toi sur l’une des 3 cas de figure du théorème des milieux, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible.
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête

