Contenu
Contraposée du Théorème de Pythagore:
Ce cours traite l’application de la Contraposée du Théorème de Pythagore. A l’aide de plusieurs exercices corrigés en vidéo, nous allons voir comment appliquer la Contraposée de Pythagore.
Contraposée et Réciproque d’un Théorème ?
Nous imaginons que nous disposons du théorème suivant : Si on a « A » alors on obtient » B « .
La Contraposée du théorème sera : » Si on n’ a pas » B » alors on n’ obtient pas « A ».
Contrairement à la Réciproque du théorème : » Si on a » B » alors on obtient « A ».
Contraposée du Théorème de Pythagore :
La Contraposée du Théorème de Pythagore permet de démontrer que le triangle n’ est pas rectangle. Par contre, la Réciproque de Pythagore est utilisée pour démontrer que le triangle est rectangle ( dans ce cas, l’égalité de Pythagore est vérifiée : le carrée de l’ hypoténuse est égal à la somme des carrées des deux autres côtés ).
Remarque : Contraposée de Pythagore ou sa Réciproque sont appliquées en connaissant les mesures des trois cotés du triangle.
Vidéo sur la Contraposée du Théorème de Pythagore :
Énonce de l’ Exercice expliqué dans la Vidéo :
DEF est un triangle et les longueurs des côtés sont : EF = 4 cm , FD = 7 cm et DE = 6 cm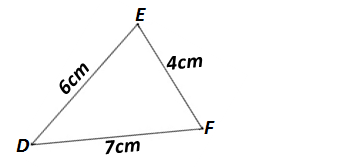
1/ si DEF est un triangle rectangle, quel côté peut être l’hypoténuse ?
2/ Est ce que le triangle DEF est rectangle ?
Correction :
1/
On sait que l’hypoténuse est le côté le plus long dans un triangle rectangle.
Donc, si le triangle DEF est rectangle, l’hypoténuse sera le côté FD = 7 cm
2/
Si le triangle DEF est rectangle, on aura l’égalité du Théorème de Pythagore : FD² = EF² + ED²
FD² = 7² = 49
EF² + ED² = 4² + 6² = 16 + 36 = 52
On remarque que : FD² ≠ EF² + ED²
Donc, d’après la Contraposée de Pythagore, ABC n’ est pas un triangle rectangle.
Exos sur la Contraposée du Théorème de Pythagore :
Exercice 1 :
Soit ABC un triangle et les longueurs de ses côtés sont : BC = 8 cm , AB = 11 cm et AC = 6 cm
Est ce que le triangle ABC est rectangle ?
Corrigé :
Si le triangle ABC est rectangle, il sera rectangle en C ( car le côté le plus long est AB ) et on aura l’égalité du Théorème de Pythagore :
AB² = CA² + CB²
AB² = 11² = 121
CA² + CB² = 6² + 8² = 36 + 64 = 100
On remarque que : AB² ≠ CA² + CB²
D’après la Contraposée du Théorème de Pythagore, ABC n’ est pas un triangle rectangle.
Exercice 2 :
On a deux triangles ABD rectangle en A et le triangle BCD et on a les longueurs suivantes :
AB = 3 cm , AD = 4 cm , BC = 3 cm et DC = 4,5cm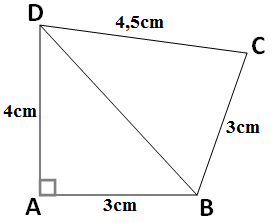
1/ Calculer la longueur du côté DB ?
2/ Est ce que le triangle BCD est rectangle ?
Corrigé :
1/
On a le triangle ABD rectangle en A.
D’après le Théorème de Pythagore :
DB² = AB² + AD² = 3² + 4² = 9 + 16 = 25
Donc, DB = 5 cm
2/
On a DB = 5cm, donc, Parmi les trois côtés du triangle BCD, le côté DB est le plus grand.
Si le triangle BCD est rectangle, l’hypoténuse est le côté DB et on aura l’égalité du Théorème de Pythagore : DB² = CB² + CD²
DB² = 5² = 25
CB² + CD² = 3² + (4,5)² = 9 + 20,25 = 29,25
On remarque que : DB² ≠ CB² + CD²
Donc, d’après la Contraposée du Théorème de Pythagore, BCD n’ est pas un triangle rectangle.
Exercice 3 :
Soit EDF un triangle avec : DF = 5,4 cm ; DE = 6,4 cm et EF = 3,5 cm.
1/ Si DEF est rectangle, il peut l’être en quelle sommet ? Justifie ton choix …
2/ Est ce que le triangle DEF est rectangle en ce sommet ?
Corrigé :
1/
le sommet ou le triangle peut être rectangle est celui opposé à l’hypoténuse.
celui qui peut être l’hypoténuse ( le plus grand côté ) est le côté DE et le sommet opposé est F.
Donc, le triangle peut être rectangle en F
2/
On a d’une part DE² = (6.4)² = 40,96 et d’autre part DF² + EF² = (5.4)² + (3.5)² = 29,16 + 12,25 = 41,41.
Ainsi, on constate que DE² ≠ DF² + EF²
donc d’après la Contraposée de Pythagore, le triangle DEF n’est pas rectangle en F
Exercice 4 :
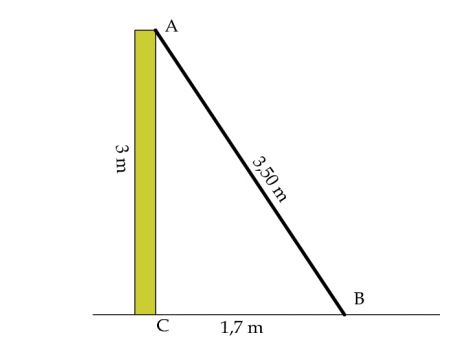
Nous avons une échelle de 3,5 m qui est placé contre un mur d’une hauteur de 3m :
- le haut de l’échelle est à la hauteur du mur.
- les pieds de l’échelle sont éloignés du mur de 1,7 m.
Est ce que le mur est perpendiculaire au sol ?
Corrigé :
Cette fois ci, c’est toi qui va le résoudre en bas en commentaire et nous te répondrons si c’est juste ou non ;).
Voici le dessin explicatif de l’exercice et qui va t’aider à bien le comprendre :
Autres liens utiles :
- Introduction sur le Théorème de Pythagore
- Calculer la longueur d’un côté dans un triangle rectangle ?
- Exercice d’ Application sur la Réciproque de Pythagore
- Théorème de Thalès
- Réciproque et Contraposée du Théorème de Thalès
Si ce n’est pas encore clair sur la Contraposée du Théorème de Pythagore, n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
