Contenu
Réciproque du Théorème de Pythagore :
Nous allons voir dans ce cours ce que c’est la Réciproque du Théorème de Pythagore à l’aide de plusieurs exercices détaillés et à la fin du cours, tu peux répondre aux exercices proposés en bas en commentaire.
Signification de la Réciproque d’un Théorème ?
Nous imaginons que nous disposons du théorème suivant : Si on a « A » alors on obtient » B « . La réciproque de ce théorème sera : » Si on a » B » alors on obtient « A ».
Réciproque du Théorème de Pythagore :
Réciproque du Théorème de Pythagore permet de démontrer qu’ un triangle est rectangle si l’égalité de Pythagore est vérifiée :
( Hypoténuse )² = ( Premier côté de l’angle droit )² + ( Deuxième côté de l’angle droit )²
» Si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et le plus grand côté est son hypoténuse « .
Par contre, la Contraposée du Théorème de Pythagoreest utilisée pour démontrer qu’ un triangle n’ est pas rectangle ( l’égalité de Pythagore n’est pas vérifié ) :
( Hypoténuse )² ≠ ( Premier côté de l’angle droit )² + ( Deuxième côté de l’angle droit )²
Vidéo : Réciproque du Théorème de Pythagore :
Enoncé de l’exercice traité dans la vidéo : ABC est un triangle et les longueurs des 3 côtés sont : AB = 5cm, AC = 3cm et BC = 4cm
Question : Est ce que le triangle ABC est rectangle ?
Correction :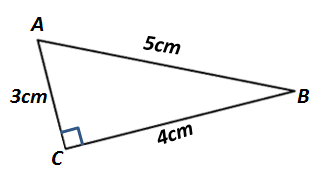
Puisque AB est le côté le plus long, si le triangle ABC est rectangle, il sera rectangle en C et on aura l’égalité du Théorème de Pythagore : AB² = CA² + CB²
On vérifie par le calcul : AB² = 5² = 25
AC² + BC² = 3² + 4² = 9 + 16 = 25
On constate que : AB² = AC² + BC²
D’après la Réciproque du Théorème de Pythagore, ABC est un triangle rectangle en C.
Autres Exos : Réciproque du Théorème de Pythagore :
Exercice 1 :
Soit ABC un triangle et les longueurs de ses côtés sont : BC = 8 cm , AC = 10 cm et AB = 6 cm
Questions :
1/ Si le triangle ABC est rectangle, il le sera en quel sommet ( A, B ou C )
2/ Démontrer que le triangle ABC est rectangle.
Réponses :
1/ Parmi les trois langueurs, AC = 10cm est la plus grande. Donc, le triangle peut être rectangle en B ( l’hypoténuse est le côté AC )
2/
On applique l’égalité du Théorème de Pythagore : AC² = BA² + BC²
On vérifie par le calcul :
On a : AC² = 10² = 100
Et : BA² + BC² = 6² + 8² = 36 + 64 = 100
On remarque que : AC² = BA² + BC²
D’après la Réciproque du Théorème de Pythagore, ABC est un triangle rectangle en B.
Exercice 2 :
Parmi les cas ci-dessous, trouve ceux qui représente un triangle rectangle. Tu laisses tes réponses justifiées en bas en commentaire et tu aura la correction.
1. Longueurs des côtés : 10 cm, 6 cm et 8 cm
2. Longueurs des côtés : 20 cm,13 cm et 15 cm
3. Longueurs des côtés : 9 cm, 3 cm et 8,5 cm.
4. Longueurs des côtés : 13 cm, 12 cm et 5 cm
5. Longueurs des côtés : 5 cm, 4 cm et 3 cm.
6. Longueurs des côtés : 20 cm, 16 cm et 12 cm
7. Longueurs des côtés : 22 cm,19 cm et 9 cm
8. Longueurs des côtés : 15 cm, 12 cm et 9 cm.
9. Longueurs des côtés : 7 cm, 5 cm et 4.5 cm
10. Longueurs des côtés : 20 cm,18 cm et 9 cm
Exercice 3 : ( Les réponses en bas en commentaire … )
Cas 1 : Construis un triangle ABC tel que : AB = 6,8 cm , BC = 10,5 cm et AC = 8 cm.
Question : Ce triangle est-il rectangle ? Justifie ta réponse.
Cas 2 : Construis un triangle DEF tel que : DE = 6,6 cm , EF = 11,2 cm et DF = 13 cm.
Question : Ce triangle est-il rectangle ? Justifie ta réponse.
Cas 3 : Construis un triangle IJK tel que : IJ = 9,1 cm , JK = 9,7 cm et IK = 13,3 cm.
Question : Ce triangle est-il rectangle ? Justifie ta réponse.
Cas 4 : Construis un triangle XYZ tel que : XY = 8,7 cm , YZ = 11,6 cm et XZ = 14,5 cm.
Question : Ce triangle est-il rectangle ? Justifie ta réponse.
Exercice 4 : ( les réponses en bas en commentaire … )
On considère deux triangle ABC et ADC tels que AB = 56, AC = 70, BC = 42, AD = 24 et DC = 74.
Démontrer que les deux triangles ABC et ADC sont rectangles ( toutes les longueurs en mm)..
Autres liens utiles :
- Introduction et Exercices d’application sur le Théorème de Pythagore
- Comment Calculer la longueur d’un côté dans un Triangle Rectangle
- Contraposée du Théorème de Pythagore
Si ce n’est pas encore clair sur Comment démontrer qu’ un triangle est rectangle à l’aide de Réciproque du Théorème de Pythagore, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
