Suites Arithmétiques – Cours sur les Suites – Première S, ES et L

Introduction sur les Suites Arithmétiques :

Parmi les suites de nombres, nous avons les suites arithmétiques qui permet de modéliser un bon nombre de situations dans notre vie courante. En cas de suites arithmétiques, on ajoute toujours le même nombre pour passer d’ un terme au suivant. Par contre, chaque terme est obtenu en multipliant le terme précédent par un nombre fixe en cas d’ une suite géométrique.

Les suites arithmétiques peut intervenir dans des cas concrets :

• Amortissement du matériels informatiques achetés par une école;
• Dans un cabinet médical, lors d’une épidémie, le nombre de patients augmente chaque jour d’un nombre fixe;
• Placer une somme d’argent dans une banque au taux d’intérêt simple de x % annuel.
• …etc

Suites Arithmétiques :

Prenons une suite numérique u_n telle que la différence entre chaque terme et son précédent est constante et égale par exemple à 7.

Le premier terme est égal à 5.

Donc, les premiers termes successifs sont : u₀ = 5, u₁ = 12, u₂ = 19, u₃ = 26, u₄ = 33, …etc. 

u₁ – u₀ = 12 – 5 = 7

u₂ – u₁ = 19 – 12 = 7

u₃ – u₂ = 26 – 19 = 7

…etc

Cette suite est appelé une suite arithmétique.

Dans notre cas, c’est une suite arithmétique de raison 7 et le premier terme est égal à 2.

La suite est donc définie par : 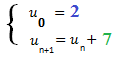Définition :

Une suite u_n est une suite arithmétique s’il existe un nombre r tel que pour tout entier n, on a : u_n+1 = u_n + r  ( r est appelé raison de la suite ).

Exercice : Démontrer si une suite est arithmétique

Nous allons montrer que la différence entre chaque terme et son précédent est constante.

Exercice 1 :

Prenons la suite (u_n) définie par : u_n = 5 – 7n.

Question : La suite u_n, , est-elle arithmétique ?

Correction :

u_n+1  –  u_n  = 5 – 7( n + 1 ) –  ( 5 – 7n )

u_n+1  –  u_n  = 5 – 7n – 7 –  5 + 7n

u_n+1  –  u_n  = -7

La différence entre un terme et son précédent est constante et égale à -7

Donc, u_n est une suite arithmétique de raison -7.

Exercice 2 :

Prenons la suite (v_n) définie par : v_n = 2 + n².

Question : la suite v_n , est-elle arithmétique ?

Correction :

v_n+1  –  v_n  = 2 + ( n + 1 )²  – ( 2 + n² )

v_n+1  –  v_n  = 2 + n² + 2n + 1 – 2 – n² 

v_n+1  –  v_n  = 2n + 1

La différence entre un terme et son précédent n’est pas constante.

Donc, v_n n’est pas une suite arithmétique.

Démonstration : 

Une suite arithmétique (u_n) de raison r et de premier terme u₀ vérifie la relation : u_n  =  u₀  + nr

On calcule les termes un par un de 0 à n :

u₁  =  u₀  + r

u₂  =  u₁  + r  = (u₀  + r ) + r = u₀  + 2r      ( On remplace u₁  par l’ expression de u₀ )

u₃  =  u₂  + r  = (u₀  + 2r ) + r = u₀  + 3r     ( On remplace u₂  par l’ expression de u₁ )

u₄  =  u₃  + r  = (u₀  + 3r ) + r = u₀  + 4r     ( On remplace u₃ par l’ expression de u₂ )

…

u_n  =  u_n-1  + r =   (u₀  + ( n-1)r ) + r =  u₀  + nr – r + r = u₀  + nr

Exercice d’ application :

Nous allons déterminer la raison et le premier terme d’une Suite Arithmétique

Considérons la suite arithmétique (u_n) tel que u₅ = 7 et u₉ = 19 .

1) Déterminer la raison et le premier terme de la suite (u_n).

2) Exprimer u_n en fonction de n.

Correction :

1)

Les termes de la suite arithmétique u_n ont  la forme suivant : u_n = u₀ + nr

Donc :   u₅ = u₀ + 5r =  7    et     u₉ = u₀ + 9r =  19

On soustrait membre à membre pour calculer la raison r :

                     u₉ – u₅ = 19 – 7

⟺ u₀ + 9r – u₀ – 5r = 12

⟺               9r –  5r = 12

⟺                       4r = 12

                              r = 3

On calcule le premier terme u₀ :

On a :  u₅ = u₀ + 5r =  7  et on remplace la valeur de la raison r :

u₀ + 5 × 3 = 7 

⟺        u₀ = 7 – 15

⟺        u₀ = -8

2)

u_n = u₀ + nr    soit    u_n =  -8 + n x 3  = – 8 + 3n 

Donc :   u_n = – 8 + 3n   ( On dit que u_n est exprimée en fonction de n )

Variations des Suites Arithmétiques

Propriété :

u_n est une suite arithmétique de raison r.

– Si r > 0 alors la suite (u_n) est croissante.

– Si r < 0 alors la suite (u_n) est décroissante.

Démonstration :  

u_n+1 –  u_n  = u_n  +  r  –  u_n = r

– Si r > 0 alors  u_n+1 –  u_n  > 0 et la suite (u_n) est croissante.

– Si r < 0 alors  u_n+1 –  u_n  < 0 et la suite (u_n) est décroissante.

Exemples :

u_n définie par u_n =  12 + 7n est suite arithmétique croissante car la raison est positive et égale à 7.

v_n définie par v_n =  7 – 5n est une suite arithmétique décroissante car la raison est négative et égale à -5.

Représentation graphique :

On appelle la représentation graphique d’ une suite ( u_n ) , l’ ensemble des points du plan de coordonnées ( n ; u_n ) 

Ci-dessous, on a représenté une suite arithmétique de raison -2 et le premier terme u₀ est égal à 5 (  u_n = 5 – 2n  ) : 

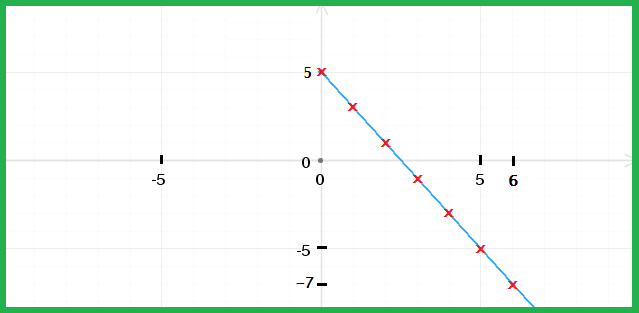
On a :   u₀ = 5   ;   u₁ = 3  ;  u₂ = 1  ;  u₃ = -1  ; u₄ = -3  ;  u₅ = -5  ; u₆ = -7 ; …

La représentation graphique de la suite ( u_n ) est l’ ensemble des points alignés en rouge pour les valeurs de n allant de 0 à 6.

Aussi, lorsque la représentation graphique d’ une suite est constituée de points alignés, cette suite est dite arithmétique.

---

Autres liens utiles :

• Exercices corrigés suites arithmétiques ( Première S ES L )
• Voir le cours sur les suites Géométriques ( Première S ES et L )
• Somme de Termes d’une suite Arithmétique / Géométrique ( Première S )

---

Au cas où tu as des questions sur les suites arithmétiques , n’hésite surtout pas de nous laisser un commentaire en bas de ce cours.

Si ce cours t’ a plu, tu peux le partager avec tes amis pour qu’eux aussi puissent en profiter 😉 !