Contenu
Introduction sur les Suites Géométriques:
Dans notre vie quotidienne, les suites géométriques et les suites arithmétiques permettent de modéliser beaucoup de situations. Dans le cas d’une suite géométrique, on passe au terme suivant en multipliant par le même nombre. Contrairement à une suite arithmétique ou on additionne.
Cas concrets ou les suites géométriques peuvent intervenir :
- Les prêts bancaires ou les placements financiers avec taux d’intérêts.
- Une population de bactéries se multiplie x fois tous les jours.
- …etc
Suites Géométriques:
Définition : Suite Géométrique
On considère une suite numérique (un) telle que la différence entre chaque terme et son précédent est constante et égale par exemple à 3.
Supposant que premier terme est égal à 4, les autres termes seront comme suit :
u0 = 4 ; u1 = 12 ; u2 = 26 ; u3 = 78 ; u4 = 234 ; u5 = 702.
Ce type de suite est appelée une suite géométrique.
Dans notre exemple, il s’agit d’une suite géométrique de raison 3 avec un premier terme égal à 4 :
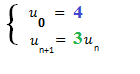 Définition :
Définition :
Une suite (un) est une suite géométrique s’il existe un nombre q tel que pour tout entier n, on a : un+1 = q x un
Le nombre q est appelé raison de la suite.
Exercice d’ application 1 : Démontrer qu’une suite est géométrique.
La suite (un) définie par : un = 5 x 7n est-elle géométrique ?
un+1 / un = 5 x 7n+1/ 5 x 7n = 7n+1/ 7n = 7
Le rapport entre un terme et son précédent reste constant et égale à 7.
Donc, (un) est une suite géométrique de raison 7 et de premier terme u0 = 5 x 70 = 5
Exemple d’ application 2 :
Supposant que l’ on a placé un capital de 600€ sur un compte dont les intérêts annuels s’élèvent à 3%.
Chaque année, le capital est multiplié par 1,03.
Ce capital suit une progression géométrique de raison 1,03.
u1 = 1,03 x 600 = 618
u2 = 1,03 x 618 = 636,54
u3 = 1,03 x 636,54 = 655,6362
De manière générale : un+1 = 1,03 x un avec u0= 600
Egalement, on peut exprimer un en fonction de n : un = 600 x 1,03n
Propriété :
(un) est une suite géométrique de raison q et de premier terme u0.
Pour tout entier naturel n, on a : un = u0 x qn
Démonstration :
La suite géométrique (un) de raison q et de premier terme u0 vérifie la relation : un+1 = q x un
On calcule les premiers termes :
u1 = q x u0
u2 = q x u1 = q x ( q x u0 ) = q² x u0
u3 = q x u2 = q x ( q² x u0 ) = q3 x u0
u4 = q x u3 = q x ( q3x u0 ) = q4 x u0
…
un = q x un-1 = q x (qn-1 u0 ) = qn x u0
Exercice d’ application :
Déterminer la raison et le premier terme d’une suite géométrique.
Considérons la suite géométrique (un) tel que u4 = 5 et u7 = 135 .
Corrigé :
Les termes de la suite (un) sont de la forme suivante : un = qn x u0
Ainsi u4 = q4 x u0 = 5 et u7 = q7 x u0 = 135.
Ainsi :
u7 / u4 = q7 x u0 / q4 x u0 = q3 et u7 / u4 = 135 / 5 = 27
Donc : q3 = 27
On utilise la fonction racine troisième de la calculatrice pour trouver le nombre qui élevé au cube donne 27 ( sinon, tu as accès gratuitement à la Calculatrice en ligne sur pigerlesmaths ).
donc : q = 3
Variations d’ une suite géométrique (Propriété)
( un) est une suite géométrique de raison q et de premier terme non nul u0.
Pour u0 > 0 :
– Si q > 1 alors la suite (un) est croissante.
– Si 0 < q < 1 alors la suite (un) est décroissante.
Pour u0 < 0
– Si q > 1 alors la suite (un) est décroissante.
– Si 0 < q < 1 alors la suite (un) est croissante.
Démonstration dans le cas où u0 > 0 :
un+1 – un = qn+1 u0 – qn u0 = u0 qn ( q – 1 )
– Si q > 1 alors un+1 – un > 0 et la suite (un) est croissante.
– Si 0 < q < 1 alors un+1 – un < 0 et la suite (un) est décroissante.
Exemple:
( un ) définie par un = – 5 x 3n est une suite géométrique décroissante car le premier terme est négatif et la raison est supérieure à 1.
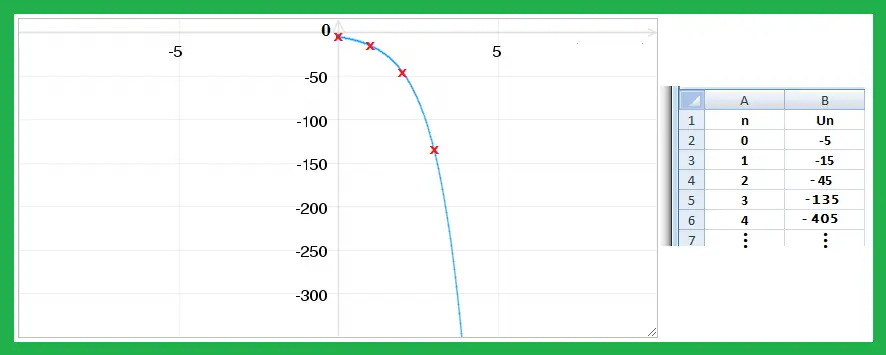
La représentation graphique ci-dessus de la suite géométrique un = – 5 x 3n est représenté par les points rouges pour les valeurs de n de 0 à 3.
Autres liens utiles :
- Cours sur les suites Arithmétiques ( Première S, ES et L )
- Exercices corrigés suites arithmétiques Première S ES L
- Somme de Termes d’une suite Arithmétique / Géométrique ( Première S )
Si tu as des questions sur les suites géométriques , n’hésite surtout pas de nous laisser un commentaire ou nous contacter sur Instagram.
Ce cours t’ a plu ?? Si c’est oui ;), tu peux le partager avec tes amis pour qu’eux aussi puissent en profiter 🙂 !

