Contenu
Exercices Suite Arithmétique Première S / ES / L
Les exercices Suite Arithmétique Première S / ES / L, traitent les points suivants :
- Comment démontrer si une suite est arithmétique ?
- Calcul de la raison et du premier terme d’ une suite arithmétique
- Etude de variations ( Croissante ou Décroissante ) d’ une suite arithmétique
- Représenter graphiquement une suite arithmétique ( forme explicite )
Démontrer Si une suite est arithmétique
Pour montrer qu’une suite ( un ) est arithmétique, il faut montrer qu’il existe un nombre réel r indépendant de n tel que, pour tout n ∈ N : un+1 = un + r
D’une autre façon, il faut montrer que la différence un+1 – un est constante : un+1 – un = r
Exercice :
1) La suite ( un ) définie par : un = 5 – 7n est-elle arithmétique ?
2) La suite ( vn ) définie par : vn = n² + 9 est-elle arithmétique ?
Corrigé :
1) un+1 – un= 5 – 7( n + 1 ) − ( 5 – 7n )
= 5 – 7n – 7 – 5 + 7n
= −7 .
La différence entre un terme et son précédent reste constante et égale à -7.
Donc, (un) est une suite arithmétique.
2)
vn+1 – vn = ( n + 1)² + 9 – ( n² + 9 )
= n² + 2n + 1 + 9 – n² – 9
= 2n + 1
La différence entre un terme et son précédent ( 2n + 1 ) ne reste pas constante car elle dépend de n.
Donc, (vn) n’est pas une suite arithmétique.
Déterminer la Raison et Premier terme
Exercice 1 :
Considérons la suite arithmétique ( un ) tel que u5 = 4 et u9 = 24 .
1) Déterminer la raison et le premier terme de la suite (un).
2) Exprimer un en fonction de n.
Corrigé :
1) Les termes de la suite sont de la forme un = u0 + nr
Ainsi u5 = u0 + 5r = 4 et u9 = u0 + 9r = 24
On soustrayant membre à membre, on obtient :
5r − 9r = 4 − 24
⇔ − 4r = -20
⇔ r = -20/-4
⇔ r = 5
Comme u0 + 5r = 4 , on a : u0 + 5 × 5 = 4 et donc : u0 = −21.
2) un = u0 + nr soit un = -21 + n × 5 ou encore un = 5n – 21
Exercice 2 :
Soit ( vn ) une suite arithmétique ayant comme second terme v1 = 5 et 9ème terme v8 = 8,5
Calculer la raison de la suite ( vn ) et le premier terme.
Corrigé :
Les termes de la suite arithmétique sont de la forme vn = v0 + nr
Ainsi v1 = v0 + r = 5 et v8 = v0 + 8r = 8.5
On soustrait membre à membre :
v1 – v8 = 5 – 8.5
⇔ v0 + r – v0 – 8r = – 3.5
⇔ r − 8r = -3.5
⇔ − 7r = -3.5
⇔ r = -3.5/-7
⇔ r = 0.5
Donc, la raison de ( vn ) est 0.5
Calcul du premier terme :
v1 = v0 + r = 5
⇔ v0 + 0.5 = 5
⇔ v0 = 5 – 0.5
⇔ v0 = 4.5
Donc, le premier terme est égal à 4.5
Etude des variations d’ une suite arithmétique
Exercice 1 :
Question : cette suite est croissante ou décroissante ?
un+1 = un + 2
u0 = 11
Corrigé :
il s’agit d’une suite définie par récurrence
On voit que la raison 2 est positive ( entre chaque terme et son suivant on rajoute 2 ) :
Donc, la suite ( un ) est Croissante
Exercice 2 :
Question : cette suite est croissante ou décroissante ?
vn+1 = vn – 5 et v0 = 7
Corrigé :
il s’agit aussi d’une suite définie par récurrence
On voit que la raison -5 est négative ( entre chaque terme et son suivant on perd -5 )
Donc, la suite ( vn ) est Décroissante
Exercice 3 :
Question : la suite wn = 3 + 2n est croissante ou décroissante ?
Corrigé :
il s’agit d’une suite exprimé en fonction de n
la raison est 2 est positive. Donc, la suite ( wn ) est Croissante
Représentation graphique suite arithmétique
Exemple : Cas suite arithmétique ayant une formule explicite
Représentation graphique de la suite (un)n∈N définie par un = 2n – 4
( un ) est une suite arithmétique de raison 2 et le premier terme est égal à – 4.
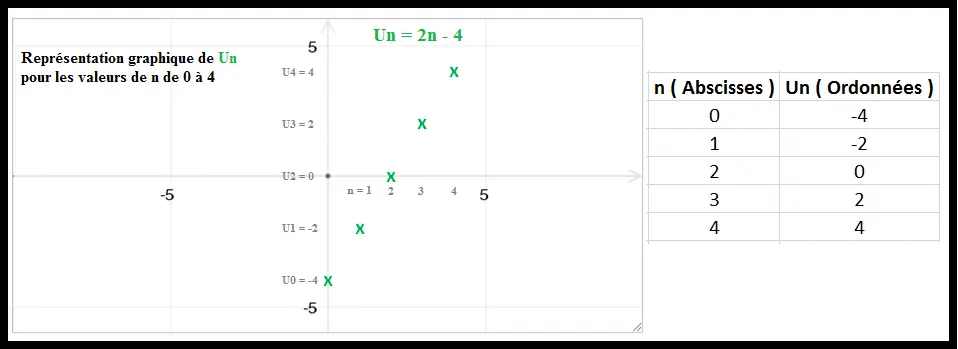
La représentation graphique de ( un ) est l’ ensemble des points alignés en verts pour les valeurs de n de 0 à 4.
Autres liens utiles sur les suites :
- Cours Suites Arithmétiques ( Première S, ES et L )
- Cours Suites Géométriques ( Première S, ES et L )
- Somme des Termes d’une suite Arithmétique ou Géométrique ( Première S )
Si tu as des questions sur l’ un des Exercices Suite Arithmétique Première S / ES / L, tout en bas, tu peux nous laisser un commentaire ;).
Bravo d’avoir lu ce cours jusqu’à la fin et tu peux le partager avec tes amis pour qu’eux aussi puissent en profiter 🙂 !
Consultez aussi notre Page Facebook de Piger-lesmaths

