La correction complète du Brevet Math 2021 pour la série générale du métropole est désormais disponible ci-dessous.
Contenu
Exercice n°1:

1) D’après le tableau, la température moyenne à Tours en novembre 2019 a été : 8,2°C.
2)
Rappel: L’ étendu d’une série statistique est la différence entre la plus grande et la plus petite valeur.
L’ étendu est égal à 22,6-4,4 = 18,2
L’étendue de cette série est de 18,2°C.
3) La formule à saisir en cellule N2 est : = MOYENNE(B2:M2) ou = SOMME(B2:M2)/12
4)
(4,4+7,8+9,6+11,2+13,4+19,4+22,6+17,9+14,4+8,2+7,8)÷12=13,1
Donc, la température moyenne annuelle est bien de 13,1°C.
5)
En cas d’ augmentation on:
La valeur d’arrivée = la valeur de départ + la valeur de départ x (P/100)
La valeur de départ est: 11,9 °C
La valeur d’arrivée est: 13,1 °C
P représente le pourcentage d’ augmentation.
Donc:
P = (la valeur d’ arrivée – la valeur de départ )x 100/ la valeur de départ
P = ( 13,1 – 11,9 )x 100 / 11,9 = 10,08
Donc le pourcentage d’augmentation entre 2009 et 2019 est d’environ 10%.
Exercice n°2:
1) 2 000 000 – 1 900 000 = 100 000
Donc, il aurait fallu 100 000 visiteurs de plus en 2019 pour atteindre 2 millions.
2)
Le nombre de jours dans une année est de 365.
1900000/365 ≈ 5 205,47
Donc, il a bien eu environ 5200 visiteurs par jour en 2019.
L’affirmation est donc vraie.
3)
a)
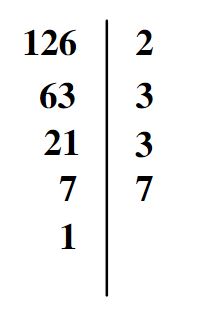
Donc: 126=2×3×3×7=2×3²×7
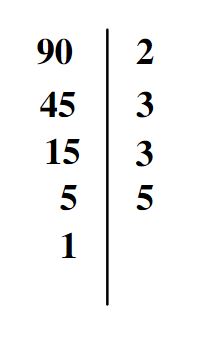
Donc: 90 =2×3×3×5 = 2×3²×5
Voir le cours sur comment décomposer un nombre en produit de facteurs premiers.
b)
Les entiers qui divisent à la fois les nombres 126 et 90 sont:
1, 2, 3, 6, 9 et 18
c) Le plus grand diviseur commun de 126 et 90 est 18.
Le professeur pourra donc constituer au maximum 18 groupes d’élèves.
126 / 18 = 7 et 90 / 18 = 5
Donc, chaque groupe sera composé de 7 garçons et 5 filles.
4) Dans les triangles ADE et ABC :
E ∈ [AB] et D ∈ [AC]
La droite (ED) est perpondiculaire à (AC)
La droite (BC) est perpondiculaire à (AC)
Donc: les deux droites (ED) et (BC) sont parallèles.
Nous pouvons donc appliquer le Théorème de Thalès dans les triangles AED et ABC et on obtient:
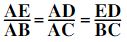
Nous avons besoin juste des deux derniers rapports:
BC= ED x AC / AD
BC= 1,60 x ( 2 + 54,25 ) / 2
BC= 45
Donc, La hauteur BC vaut 45m.
Exercice n°3:
PARTIE A :
1) Réponse C: La probabilité d’obtenir un jeton vert ( 7 jetons verts sur 16 jetons au total).
2) Réponse A:
La probabilité de ne pas tirer un jeton bleu ( Donc, on va tirer soit un jeton Vert, Rouge ou Jaune ) est:
( 7 + 4 + 2 )/16 = 13/16
PARTIE B :
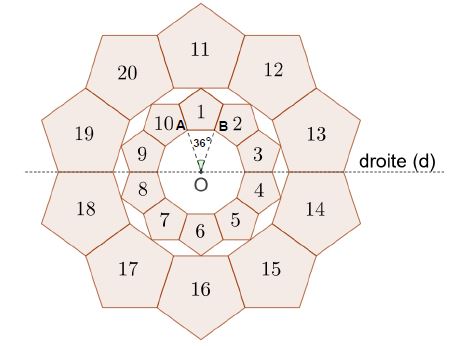
3) Réponse A: L’image du motif 20 par la symétrie d’axe la droite (d) est le motif 17.
4) Réponse B: Le motif 3 est l’image du motif 1 par une rotation de centre O, d’angle 72° dans le sens horaire.
( ou d’angle 288° dans le sens anti-horaire ).
5) Réponse B: Le motif 11 est un agrandissement du motif 1 de rapport 2.
Donc, l’aire du motif 11 est égale à 4 fois l’aire du motif 1.
Exercice n°4:
Voici le programme de calcul:
-Choisir un nombre.
-Prendre le carré du nombre de départ.
-Ajouter le triple du nombre de départ.
-Soustraire 10 au résultat.
1)
Le nombre choisi est 4
Donc: 16 + 3 x 4 – 10 = 28 − 10 = 18
Donc, si on choisi comme nombre de départ 4 on obtient bien 18.
2)
On choisissant -3 on obtient -10.
3)
4)
a) Soit x le nombre choisi au départ.
Le résultat final sera : x²+3x−10
b)
On va développer l’ expression (x+5)(x−2):
(x+5)(x−2) = x² − 2x + 5x − 10 = x² + 3x − 10
c)
On va résoudre l’ équation produit nul:
(x+5)(x−2) = 0
⇔ x+5=0 ou x−2=0
⇔ x = -5 ou x = 2
Donc, on doit choisir -5 ou 2 au départ pour obtenir 0 à l’arrivée.
Exercice n°5:
1) 5,2 x (6,5/100) = 0,338.
Donc, la production annuelle de déchets par Français en 2017 a diminué de 0,338 tonnes.
2)
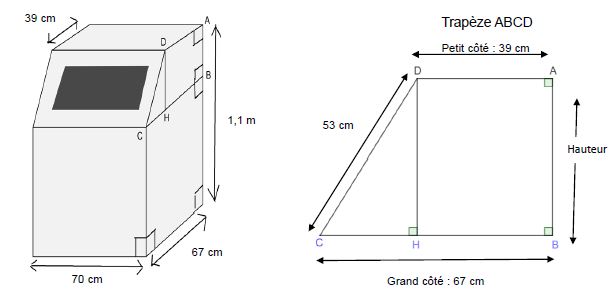
a) CH = CB − HB = 67 − 39 = 28cm.
DC² = CH² + DH²
DH² = DC² – CH²
DH² = 53² – 28²
DH² = 2809 – 784
DH² = 2025
![]()
DH = 45cm
c)
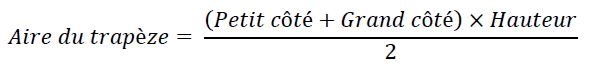
L’ aire du trapèze = ( (39 + 67) x 45 ) / 2 = 2385 cm².
d)
Donc, l’affirmation est vraie.
Si jamais tu as des questions concernant la correction Brevet Math 2021, n’ hésite pas de nous écrire en bas encommentaire.
