Nous allons voir dans ce cours, la racine carrée d’un nombre et des propriétés importantes à savoir et la simplification des expressions contenant des racines carrées.
Par exemple, les racines carrées sont utilisées dans le Théorème de Pythagore et dans la Résolution des équations du second degré.
Contenu
Racine Carrée d’un nombre
Définition :
Racine carrée d’un nombre x est le nombre positif y tel que y × y = x.
Autrement dit, Racine carrée d’un nombre positif x c’est ce nombre x à la puissance 1/2 = 0.5 :
Racine(x) = x1/2 = x 0,5
Exemples : 40,5 = 2 ; 160,5 = 4 ; 250,5 = 5 ; 640,5 = 8 ; …
Impossible de calculer la racine carrée d’un nombre négatif car le résultat du produit d’un nombre par lui-même est toujours positif.
Exemple 1 : Racine carrée de 16
Racine carrée de 16 est 4 car 4×4=16.
Exemple 2 : Racine carrée de 25
Racine carrée de 25 est 5 car 5×5=25.
Autres exemples :
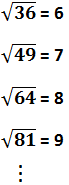
Racine Carrée et les Opérations :
Propriété 1 : Racine carrée d’ un Produit
Soit a et b deux nombres positifs :
![]()
Exemple 1 :
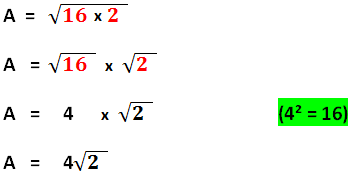
Exemple 2 :
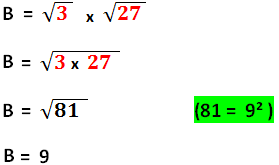
Propriété 2 : Racine carrée d’ un Quotient
Soit a et b deux nombres positifs tel que b est un nombre non Nul :
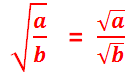
Exemple 1 :
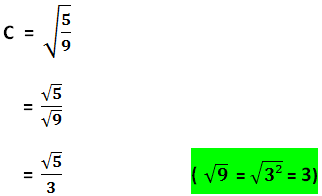
Exemple 2 :
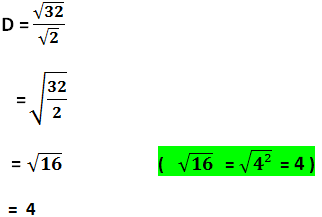
Remarque Importante :
Prenons a et b deux nombres positifs :
![]()
Exemples :
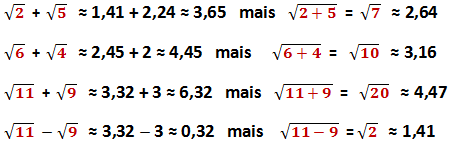
Donc, on ne peut pas additionner ou soustraire des racines carrées.
Par contre, dans certains cas, il est possible d’additionner des racines carrées en transformant leurs écritures pour faire apparaître la racine d’un même nombre.
Regroupement et Simplification de racines carrées :
En faisant la simplification des expressions contenant des racines carrées, on sera toujours amener à appliquer les règles d’ Addition des nombres relatifs.
Exemples d’ application :
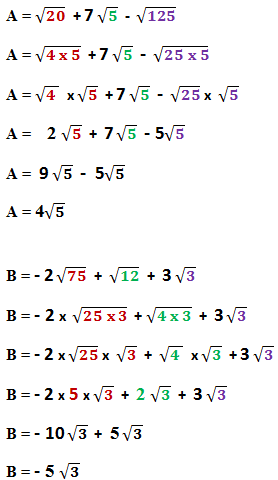
Autres liens utiles :
- Calcul de puissance et comment déterminer le signe ?
- Comment calculer les puissances de 10 ?
- Calcul du produit des puissances
- Calculer le quotient de deux puissances
Si ce Cours n’est pas encore clair pour toi, n’hésite surtout pas de laisser un commentaire en bas.
Consultez aussi notre Page Facebook de Piger-lesmaths

