Nous allons voir dans ce cours, comment dessiner deux droites Parallèles et Perpendiculaires et aussi les quatre propriétés qui sont très importantes en géométrie. En Brevet par exemple, tu peux avoir besoin de ces propriétés dans un exercice sur le Théorème de Thalès.
Contenu
Droites Parallèles et Perpendiculaires ( Définitions ) :
Droites Parallèles :
Deux droites distinctes ayant aucun point en commun sont dites parallèles.
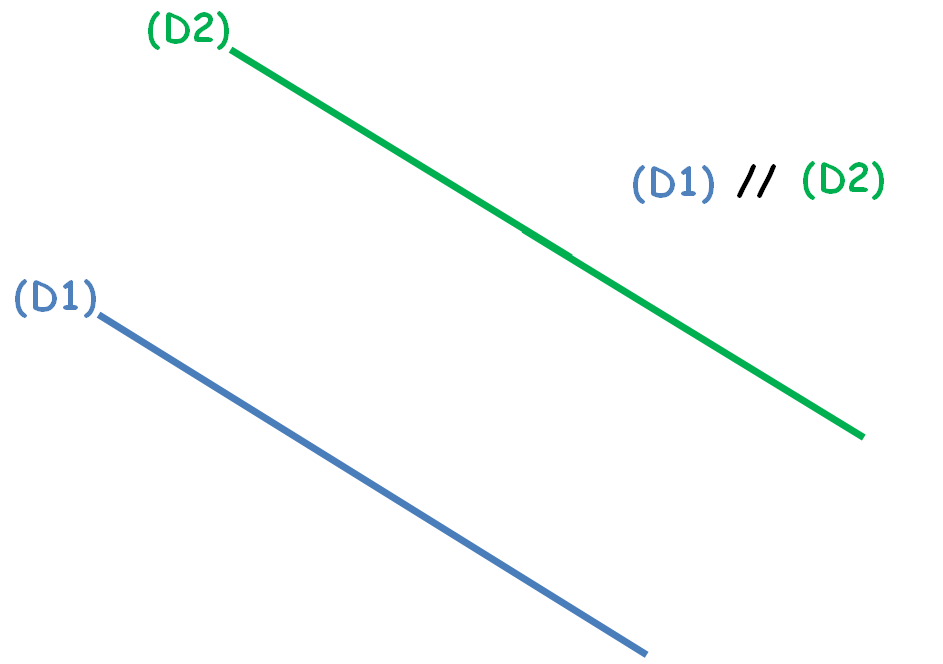 Deux droites (D1) et (D2) Parallèles est noté : ( D1 ) // ( D2 )
Deux droites (D1) et (D2) Parallèles est noté : ( D1 ) // ( D2 )
Droite Parallèle Passant par un Point donné :
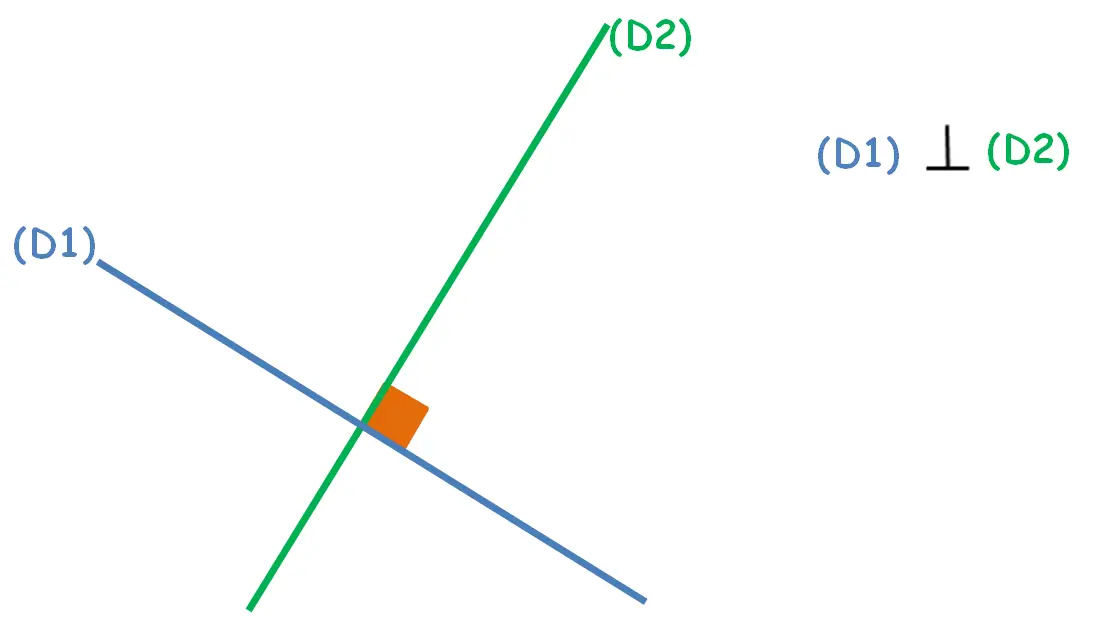
Droites perpendiculaires :
Si deux droites se coupent en formant un angle droit, sont perpendiculaires.
Deux droites (D1) et (D2) Perpendiculaires est noté : ( D1 ) ⊥ ( D2 ).
Droite Perpendiculaire Passant par un Point donné :
Droites Parallèles et Perpendiculaires ( Propriétés ) :
Il y’a quatre propriétés importantes liées aux droites Parallèles et Perpendiculaires.
Propriété 1 : Droites Parallèles
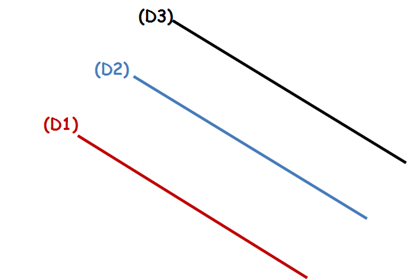
Prenons deux droites Parallèles : (D1) //(D2). Si une troisième droite (D3) est Parallèle à l’une des deux droites (D1) ou (D2), il sera Parallèle à l’autre :
Si (D1) // (D2) Et (D3) ⊥ (D1) Alors (D3) // (D2)
Concernant la 2ème, la 3ème et la 4ème propriété, on considère la figure ci-dessous :
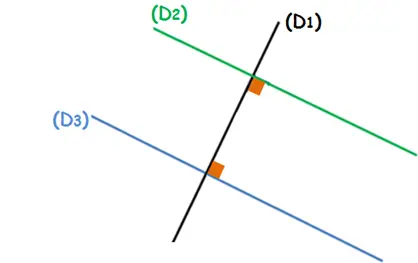
Propriété 2 :
Prenons deux droites Parallèles : (D1) // (D2). Si une troisième droite (D3) est Perpendiculaire à l’une des deux droites (D1) ou (D2), il sera Perpendiculaire à l’autre :
Si (D1) // (D2) Et (D3) ⊥ (D1) Alors (D3) ⊥ (D2)
Propriété 3 :
Prenons deux droites Perpendiculaires (D1) et (D2). Si une troisième droite (D3) est Parallèle à l’une des deux droites (D1) ou (D2), il sera Perpendiculaire à l’autre :
Si (D1) ⊥ (D2) Et (D3) // (D2) Alors (D3) ⊥ (D1)
Propriété 4 :
Prenons deux droites Perpendiculaires (D1) et (D2). Si une troisième droite (D3) est Perpendiculaire à l’une des deux droites (D1) ou (D2), il sera Parallèle à l’autre :
Si (D1) ⊥ (D2) Et (D3) ⊥ (D1) Alors (D3) // (D2)
Autres liens utiles :
- Comprendre le théorème de Thalès ( Niveau 3ème )
- Comprendre le théorème de Pythagore ( Niveau 4 et 3ème )
- Voir toutes nos vidéos sur le Théorème de Pythagore ( Niveau 4 et 3ème )
Si ce n’est pas encore clair sur les Droites Parallèles et Perpendiculaires , n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête