Contenu
Comment Réduire au même dénominateur ?
Pour réduire au même dénominateur deux fractions ayant deux dénominateurs différents, on cherche le plus petit multiple commun des deux dénominateurs.
Règle fondamentale pour les fractions ( Rappel ) : quand on multiplie (ou on divise) le numérateur et le dénominateur d’une fraction par un même nombre non nul, la fraction reste toujours la même ( voir la vidéo dissous ) :
Les deux exemples traités dans la vidéo ci-dessous :
Exemple 1 : Réduire au même dénominateur 7/2 et 2/3
Exemple 2 : Réduire au même dénominateur 2/7 et 5/4
Solution ( Exemple 1 ):
On réduit au même dénominateur les deux fractions :
Les multiples de 2 : 2 ; 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 ; …
Les multiples de 3 : 3 ; 6 ; 12 ; 18 ; 24 ; …
==> Le plus petit multiple commun est 6 :
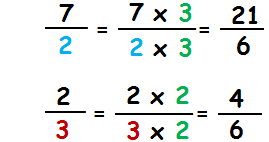
On voit maintenant que les deux fractions 21/6 et 4/6 ont le même dénominateur qui est 6.
Solution ( Exemple 2 ) :
On réduit au même dénominateur les deux fractions :
Les multiples de 7 : 7 ; 14 ; 21 ; 28 ; 10 ; 12 ; 14 ; 16 ; …
Les multiples de 4 : 4 ; 8 ; 12 ; 16 ; 20 ; 24 ; 28 ; 32 ; …
==> Le plus petit multiple commun est 28 :
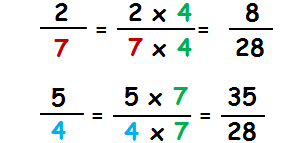
On voit maintenant que les deux fractions 8/28 et 35/28 ont le même dénominateur qui est 28
Exercices à Faire :
Nous t’invitons à réduire au même dénominateur les exemples ci-dessous et tu peux laisser tes réponses en bas en commentaire :
1/ 7/2 et 8/3
2/ 11/5 et 9/7
3/ 6/10 et 9/8
4/ 23/12 et 5/4
Autres liens utiles :
Si ce n’est pas encore clair sur Comment réduire au même dénominateur deux fractions, n’hésite surtout pas de nous laisser un commentaire en bas et nous te répondrons le plutôt possible.
Consultez aussi la Page Facebook de Piger-lesmaths et Youtube
