Nous allons voir dans ce cours, différents aspects sur les nombres complexes : Ensemble des nombres complexes ℂ, Forme Algébrique, L’ inverse, le Conjugué et le Module d’ un nombre complexe avec des exemples détaillés.
Contenu
Définition de l’ Ensemble des Nombres Complexes ℂ
Il existe un ensemble de nombres, noté ℂ, appelé ensemble des nombres complexes qui possède les propriétés suivantes :
– ℂ contient ℝ.
– Dans ℂ, on définit une addition et une multiplication qui suivent les mêmes règles de calcul que dans ℝ.
– Il existe dans ℂ un nombre i tel que i² = -1
– Tout élément z de ℂ s’écrit de manière unique sous la forme ( dite Forme Algébrique ) :
a + ib avec a et b qui sont des nombres réels.
Forme Algébrique d’un Nombre Complexe
La forme algébrique d’un nombre complexe est a + ib où a et b sont deux nombres réels.
Si z = a + ib ( où a et b sont deux nombres réels )
a représente la partie réelle de z, notée Re(z).
b représente la partie imaginaire de z, notée Im(z).
On peut écrire : Re(z) = a et Im(z) = b
Remarques :
– Le nombre z est réel si et seulement si Im (z) = 0
– Le nombre z est Imaginaire Pur si et seulement si Re (z) = 0
Exemple 1 :
Soit le nombre complexe suivant : -13 + 5i
La partie réelle du nombre z est : Re(z) = -13
La partie imaginaire du nombre z est : Im(z) = 5
Exemple 2 :
Soit le nombre complexe suivant : -7 – 19i
La partie réelle du nombre z est : Re(z) = -7
La partie imaginaire du nombre z est : Im(z) = -19
Autres Exemples : Nombre Complexe sous forme Algébrique
A = 3 – 5i – ( 3i – 4 ) = ?
B = ( 3 -2i )(-1 +5i ) = ?
C = ( 2 – 3i )² = ?
D = ( 3i )5 = ?
Correction :
A = 3 – 5i – ( 3i – 4 )
A = 3 – 5i – 3i + 4
A = 7 – 8i
Donc :
La partie réelle du nombre z est : Re(z) = 7
La partie imaginaire du nombre z est : Im(z) = – 8
B = ( 3 – 2i )( -1 + 5i )
B = -3 + 15i +2i +10
B = 7 + 17i
Donc :
La partie réelle du nombre z est : Re(z) = 7
La partie imaginaire du nombre z est : Im(z) = 17
C = ( 2 – 3i )²
C = 2² + ( 3i )² – 2*2*(3i) ( Identité Remarquable )
C = 4 – 9 – 12i
C = – 5 – 12i
Donc :
La partie réelle du nombre z est : Re(z) = – 5
La partie imaginaire du nombre z est : Im(z) = – 12
D = ( 3i )5
D = 35 * i 5
D = 243 * i
D = 243i
Donc :
La partie réelle du nombre z est : Re(z) = 0
La partie imaginaire du nombre z est : Im(z) = 243
Pourquoi : i5 = i ?
i5 = i² * i² * i = (-1) * (-1) * i = 1 * i = i
Nombre Complexe Égaux ? ( Théorème )
On dit que deux nombres complexes sont égaux si et seulement s’ ils ont la même partie réelle et la même partie imaginaire.
Inverse d’ un nombre Complexe :
Soit z est un nombre complexe non nul. il existe un nombre complexe z’ tel que z*z’ = zz’ = 1.
Le nombre complexe z’ représente l’ inverse de z : z’ = 1/z
Exemple : l’ inverse de i est -i
i * ( -i ) = – i * i = – ( -1 ) = 1
Conjugué d’ un Nombre Complexe :
Définition :
Soit z un nombre complexe : z = a + ib ( où a et b sont deux nombres réels )
Le nombre complexe conjugué de z est le nombre noté :
![]()
Exemples : Conjugué de Nombres Complexes

Propriétés des Conjugués :
Pour tous nombres complexes z et z’ et tout entier naturel n :
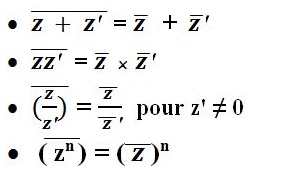
Module d’ un Nombre Complexe :
Définition :
Soit z = a + b i ( où a et b sont deux nombres réels et z est sous la forme algébrique ).
On appelle le module du nombre complexe z, le nombre réel défini par :
![]()
Remarques :
– Le module d’un nombre complexe est un réel positif.
– Deux nombres complexes distincts peuvent avoir le même module :
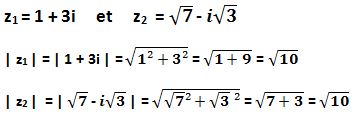
Exo : Calcul du Module des Nombres Complexes
Calcul du module des exemples suivants :
| 1 + 4i | = ?
| 3 – 5i | = ?
![]()
| -7 | = ? ( -7 est un Nombre réel car Im ( -7 ) = 0 )
| – 6i | = ? ( -6i est un Imaginaire Pur car Re( -6i ) = 0 )
![]()
Correction :
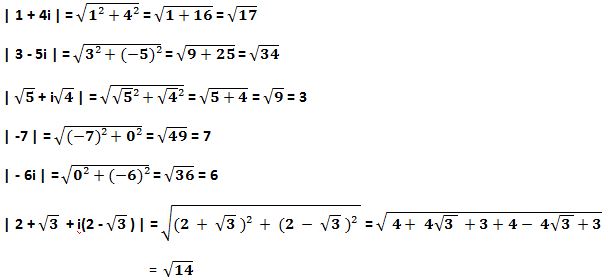
Autres liens utiles :
- Un peu d’ Histoire des algébristes Italiens et les Nombres Complexes
- Solutions des équations du second degré dans l’ Ensemble ℂ
