Contenu
Angle inscrit et Angle au centre ( Définitions ) :
Dans un cercle, les théorèmes de l’ angle inscrit et angle au centre établissent des relations qui relient les angles inscrits et les angles au centre interceptant le même arc.
Angle Inscrit :
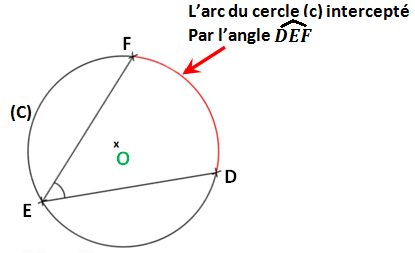
On a un cercle (C) de centre O et les points D, E et F appartiennent à ce cercle.
L’ angle [latex]\widehat{DEF}[/latex] est appelé l’ angle inscrit dans le cercle (C).
L’arc FD qui ne contient pas E est appelé l’arc de cercle (C) intercepté par l’angle [latex]\widehat{DEF}[/latex].
Angle au Centre :
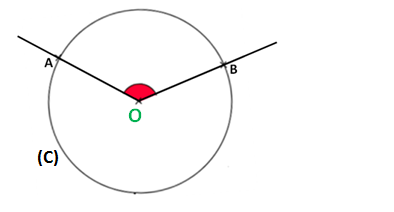
L’angle au centre est un angle dont le sommet est le centre du cercle.
L’angle [latex]\widehat{BOA}[/latex] est un angle au centre.
Propriétés :
Propriété ( Angle inscrit et angle au centre ) :
La mesure d’un angle inscrit dans un cercle (C) est La moitié de la mesure de l’angle au Centre qui intercepte le même arc.
Dans notre cas :
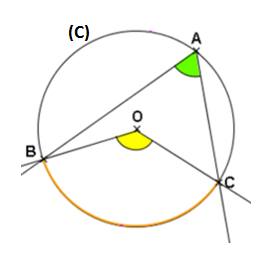
L’angle inscrit [latex]\widehat{BAC}[/latex] intercepte l’arc BC et l’angle au centre [latex]\widehat{BOC}[/latex] intercepte le même arc.
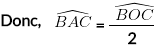
Propriété ( Angles Inscrits ) :
Angles inscrits au même cercle (C) et qui interceptent le même arc, ont la même mesure.
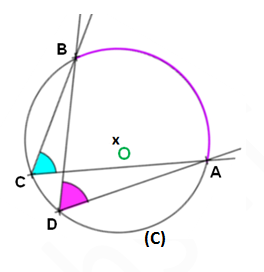
On considère le cas de la figure ci-dessous :
L’angle inscrit [latex]\widehat{ADB}[/latex] intercepte l’arc BA et l’angle inscrit [latex]\widehat{ACB}[/latex] intercepte le même arc BA.
Donc, [latex]\widehat{ADB}[/latex] = [latex]\widehat{ACB}[/latex]
Triangle Inscrit dans un cercle :
Propriété :
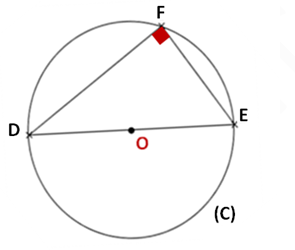
Quand on joint un point d’un cercle aux extrémités de son diamètre, le triangle ainsi formé est rectangle. Le diamètre du cercle est son Hypoténuse.
Dans notre cas, le côté DE représente le diamètre du cercle. Donc, DEF est rectangle en F (L’ hypoténuse est le côté DE).
A quoi sert cette Propriété ?
Cette propriété sert à montrer qu’ un triangle est rectangle.
Exercice d’application :
Lesquels des 3 triangles inscrits (Marron, Bleu et Vert ) dans le cercle (C) est rectangle en expliquant pourquoi ?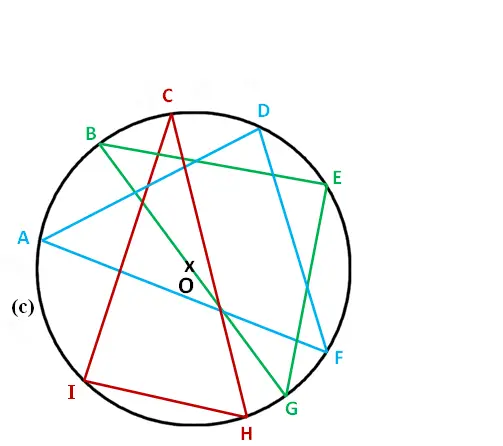
Solution :
- ADF n’est pas un triangle rectangle car aucun de ses côtés ne représente un diamètre.
- CHI n’est pas un triangle rectangle car aucun de ses côtés ne représente un diamètre.
- BEG est un triangle rectangle en E car le côté BG est un diamètre du cercle (C)
( Donc, BG représente l’Hypoténuse du triangle BEG ).
Autres liens utiles :
Si ce n’est pas encore clair pour toi sur l’ angle inscrit et angle au centre, n’hésite surtout pas de laisser un commentaire en bas et nous te répondrons le plutôt possible :).
Sinon, après avoir lu ce cours, écris le mot qui te passe à la tête
